Wavelet Families
The Wavelet Toolbox™ software includes a large number of wavelets that you can use for both continuous and discrete analysis. For discrete analysis, examples include orthogonal wavelets (Daubechies’ extremal phase and least asymmetric wavelets) and B-spline biorthogonal wavelets. For continuous analysis, the Wavelet Toolbox software includes Morlet, Meyer, derivative of Gaussian, and Paul wavelets.
The choice of wavelet is dictated by the signal or image characteristics and the nature of the application. If you understand the properties of the analysis and synthesis wavelet, you can choose a wavelet that is optimized for your application.
Wavelet families vary in terms of several important properties. Examples include:
Support of the wavelet in time and frequency and rate of decay.
Symmetry or antisymmetry of the wavelet. The accompanying perfect reconstruction filters have linear phase.
Number of vanishing moments. Wavelets with increasing numbers of vanishing moments result in sparse representations for a large class of signals and images.
Regularity of the wavelet. Smoother wavelets provide sharper frequency resolution. Additionally, iterative algorithms for wavelet construction converge faster.
Existence of a scaling function, φ.
For continuous analysis, the Wavelet Toolbox software analytic wavelet-based analysis for select wavelets. See
cwt and icwt for details. Inverse Continuous Wavelet Transform for a
basic theoretical motivation. CWT-Based Time-Frequency Analysis illustrates the use of the
continuous wavelet transform for simulated and real-world signals.
Entering waveinfo at the
command line displays a survey of the main properties of available
wavelet families. For a specific wavelet family, use waveinfo with
the wavelet family short name. You can find the wavelet family short
names listed in the following table and on the reference page for waveinfo.
Wavelet Family Short Name | Wavelet Family Name |
|---|---|
'haar' | Haar wavelet |
'db' | Daubechies wavelets |
'sym' | Symlets |
'coif' | Coiflets |
'bior' | Biorthogonal wavelets |
'rbio' | Reverse biorthogonal wavelets |
'meyr' | Meyer wavelet |
'dmey' | Discrete approximation of Meyer wavelet |
'gaus' | Gaussian wavelets |
'mexh' | Mexican hat wavelet (also known as the Ricker wavelet) |
'morl' | Morlet wavelet |
'cgau' | Complex Gaussian wavelets |
'shan' | Shannon wavelets |
'fbsp' | Frequency B-Spline wavelets |
'cmor' | Complex Morlet wavelets |
'fk' | Fejer-Korovkin wavelets |
To display detailed information about the Daubechies’ least asymmetric orthogonal wavelets, enter:
waveinfo('sym')To compute the wavelet and scaling function (if available),
use wavefun.
The Morlet wavelet is suitable for continuous analysis. There is no scaling function associated with the Morlet wavelet. To compute the Morlet wavelet, you can enter:
[psi,xval] = wavefun('morl',10); plot(xval,psi); title('Morlet Wavelet');
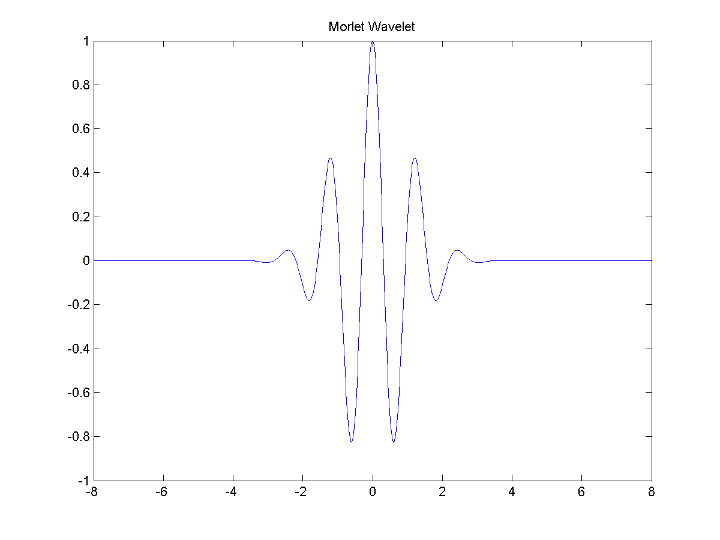
For wavelets associated with a multiresolution analysis, you can compute both the scaling function and wavelet. The following code returns the scaling function and wavelet for the Daubechies’ extremal phase wavelet with 4 vanishing moments.
[phi,psi,xval] = wavefun('db4',10); subplot(211); plot(xval,phi); title('db4 Scaling Function'); subplot(212); plot(xval,psi); title('db4 Wavelet');

In discrete wavelet analysis, the analysis and synthesis filters
are of more interest than the associated scaling function and wavelet.
You can use wfilters to obtain
the analysis and synthesis filters.
Obtain the decomposition (analysis) and reconstruction (synthesis) filters for the B-spline biorthogonal wavelet. Specify 3 vanishing moments in the synthesis wavelet and 5 vanishing moments in the analysis wavelet. Plot the filters’ impulse responses.
[LoD,HiD,LoR,HiR] = wfilters('bior3.5'); subplot(221); stem(LoD); title('Lowpass Analysis Filter'); subplot(222); stem(HiD); title('Highpass Analysis Filter'); subplot(223); stem(LoR); title('Lowpass Synthesis Filter'); subplot(224); stem(HiR); title('Highpass Synthesis Filter');

Daubechies Wavelets: dbN
The dbN wavelets are the Daubechies’
extremal phase wavelets. N refers to the number
of vanishing moments. These filters are also referred to in the literature
by the number of filter taps, which is 2N. More
about this family can be found in [Dau92] page 195. Enter waveinfo('db') at
the MATLAB® command prompt to obtain a survey of the main properties
of this family.
Daubechies Wavelets db4 on the Left and db8 on the Right

The db1 wavelet is also known as the Haar wavelet. The Haar wavelet is the only orthogonal
wavelet with linear phase. Using waveinfo('haar'),
you can obtain a survey of the main properties of this wavelet.
Symlet Wavelets: symN
The symN wavelets are also known as Daubechies’
least-asymmetric wavelets. The symlets are more symmetric than the
extremal phase wavelets. In symN, N is
the number of vanishing moments. These filters are also referred to
in the literature by the number of filter taps, which is 2N.
More about symlets can be found in [Dau92], pages 198, 254-257. Enter waveinfo('sym') at
the MATLAB command prompt to obtain a survey of the main properties
of this family.
Symlets sym4 on the Left and sym8 on the Right

Coiflet Wavelets: coifN
Coiflet scaling functions also exhibit vanishing moments. In coifN, N is
the number of vanishing moments for both the wavelet and scaling functions.
These filters are also referred to in the literature by the number
of filter coefficients, which is 3N. For the coiflet
construction, see [Dau92] pages 258–259. Enter waveinfo('coif') at
the MATLAB command prompt to obtain a survey of the main properties
of this family.
Coiflets coif3 on the Left and coif5 on the Right
If s is a sufficiently regular continuous time signal, for large j the coefficient is approximated by .
If s is a polynomial of degree d, d ≤ N – 1, the approximation becomes an equality. This property is used, connected with sampling problems, when calculating the difference between an expansion over the φj,l of a given signal and its sampled version.
Biorthogonal Wavelet Pairs: biorNr.Nd
While the Haar wavelet is the only orthogonal wavelet with linear phase, you can design biorthogonal wavelets with linear phase.
Biorthogonal wavelets feature a pair of scaling functions and associated scaling filters — one for analysis and one for synthesis.
There is also a pair of wavelets and associated wavelet filters — one for analysis and one for synthesis.
The analysis and synthesis wavelets can have different numbers of vanishing moments and regularity properties. You can use the wavelet with the greater number of vanishing moments for analysis resulting in a sparse representation, while you use the smoother wavelet for reconstruction.
See [Dau92] pages 259, 262–285 and [Coh92] for more details
on the construction of biorthogonal wavelet bases. Enter waveinfo('bior') at
the command line to obtain a survey of the main properties of this
family.
The following code returns the B-spline biorthogonal reconstruction and decomposition filters with 3 and 5 vanishing moments and plots the impulse responses.
The impulse responses of the lowpass filters are symmetric with respect to the midpoint. The impulse responses of the highpass filters are antisymmetric with respect to the midpoint.
[LoD,HiD,LoR,HiR] = wfilters('bior3.5'); subplot(221); stem(LoD); title('Lowpass Analysis Filter'); subplot(222); stem(HiD); title('Highpass Analysis Filter'); subplot(223); stem(LoR); title('Lowpass Synthesis Filter'); subplot(224); stem(HiR); title('Highpass Synthesis Filter');

Reverse Biorthogonal Wavelet Pairs: rbioNr.Nd
This family is obtained from the biorthogonal wavelet pairs previously described.
You can obtain a survey of the main properties of this family
by typing waveinfo('rbio') from the MATLAB command
line.
Reverse Biorthogonal Wavelet rbio1.5

Meyer Wavelet: meyr
Both ψ and φ are defined in the frequency domain,
starting with an auxiliary function ν (see [Dau92] pages 117,
119, 137, 152). By typing waveinfo('meyr') at the MATLAB command
prompt, you can obtain a survey of the main properties of this wavelet.
Meyer Wavelet

The Meyer wavelet and scaling function are defined in the frequency domain:
Wavelet function
and
where
Scaling function
By changing the auxiliary function, you get a family of different wavelets. For the required properties of the auxiliary function ν, see References for more information. This wavelet ensures orthogonal analysis.
The function ψ does not have finite support, but ψ
decreases to 0 when ![]() , faster than any inverse polynomial
, faster than any inverse polynomial
such that
This property holds also for the derivatives
, such that
The wavelet is infinitely differentiable.
Note
Although the Meyer wavelet is not compactly supported, there
exists a good approximation leading to FIR filters that you can use
in the DWT. Enter waveinfo('dmey') at the MATLAB command
prompt to obtain a survey of the main properties of this pseudo-wavelet.
Gaussian Derivatives Family: gaus
This family is built starting from the Gaussian function by taking the pth derivative of f.
The integer p is the parameter of this family and in the previous formula, Cp is such that where f (p) is the pth derivative of f.
You can obtain a survey of the main properties of this family
by typing waveinfo('gaus') from the MATLAB command
line.
Gaussian Derivative Wavelet gaus8

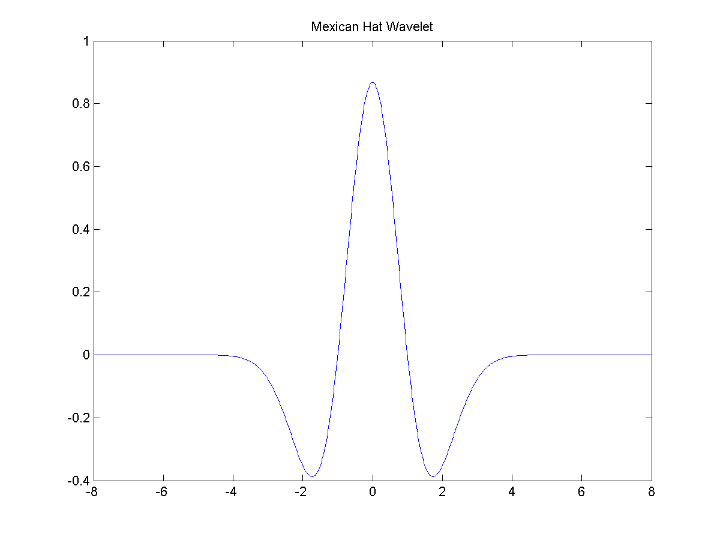
Mexican Hat Wavelet: mexh
This wavelet is proportional to the second derivative function of the Gaussian probability density function. The wavelet is a special case of a larger family of derivative of Gaussian (DOG) wavelets. It is also known as the Ricker wavelet.
There is no scaling function associated with this wavelet.
Enter waveinfo('mexh') at the MATLAB command
prompt to obtain a survey of the main properties of this wavelet.
You can compute the wavelet with wavefun.
[psi,xval] = wavefun('mexh',10); plot(xval,psi); title('Mexican Hat Wavelet');
Morlet Wavelet: morl
Both real-valued and complex-valued versions of this wavelet
exist. Enter waveinfo('morl') at the MATLAB command
line to obtain the properties of the real-valued Morlet wavelet.
The real-valued Morlet wavelet is defined as:
The constant C is used for normalization in view of reconstruction.
[psi,xval] = wavefun('morl',10); plot(xval,psi); title('Real-valued Morlet Wavelet');

The Morlet wavelet does not technically satisfy the admissibility condition..
Additional Real Wavelets
Some other real wavelets are available in the toolbox.
Complex Wavelets
The toolbox also provides a number of complex-valued wavelets for continuous wavelet analysis. Complex-valued wavelets provide phase information and are therefore very important in the time-frequency analysis of nonstationary signals.
Complex Gaussian Wavelets: cgau
This family is built starting from the complex Gaussian function
by taking the pth derivative of f. The integer p is the parameter of this family and in the previous formula, Cp is such that
where f (p) is the pth derivative of f.
You can obtain a survey of the main properties of this family
by typing waveinfo('cgau') from the MATLAB command
line.
Complex Gaussian Wavelet cgau8
Complex Morlet Wavelets: cmor
See [Teo98] pages 62–65.
A complex Morlet wavelet is defined by
depending on two parameters:
fb is a bandwidth parameter.
fc is a wavelet center frequency.
You can obtain a survey of the main properties of this family
by typing waveinfo('cmor') from the MATLAB command
line.
Complex Morlet Wavelet morl 1.5-1

Complex Frequency B-Spline Wavelets: fbsp
See [Teo98] pages 62–65.
A complex frequency B-spline wavelet is defined by
depending on three parameters:
m is an integer order parameter (m ≥ 1).
fb is a bandwidth parameter.
fc is a wavelet center frequency.
You can obtain a survey of the main properties of this family
by typing waveinfo('fbsp') from the MATLAB command
line.
Complex Frequency B-Spline Wavelet fbsp 2-0.5-1

Complex Shannon Wavelets: shan
See [Teo98] pages 62–65.
This family is obtained from the frequency B-spline wavelets by setting m to 1.
A complex Shannon wavelet is defined by
depending on two parameters:
fb is a bandwidth parameter.
fc is a wavelet center frequency.
You can obtain a survey of the main properties of this family
by typing waveinfo('shan') from the MATLAB command
line.
Complex Shannon Wavelet shan 0.5-1
