3D plot from imported Excel data
Accepted Answer
More Answers (3)
5 votes
Your variable Z is still a column vector, since size(test,2) is 3 and thus the column index 3:size(test,2) is still just 3. You're replicating the vectors x and y to create a set of matrices X and Y when you use MESHGRID, and since z is still a vector, and not a matrix of the same size as X and Y, you can't plot a mesh.
This is a guess, but it sounds like what you actually have is a set of x, y, and z data that represent 3-D points scattered in space that lie on a surface. To plot this surface as a mesh, you have to define some sort of connectivity between them. There are a couple ways to do this:
- Plot a triangular mesh: You can connect your x and y points into a 2-D triangular mesh using the function DELAUNAY, then plot a 3-D mesh using the function TRIMESH:
x = rand(100,1); % Sample x data y = rand(100,1); % Sample y data z = exp(-(x-0.5).^2-(y-0.5).^2); % Sample z data (a 2-D Gaussian) tri = delaunay(x,y); % Create a 2-D triangular mesh trimesh(tri,x,y,z); % Plot the mesh in 3-D
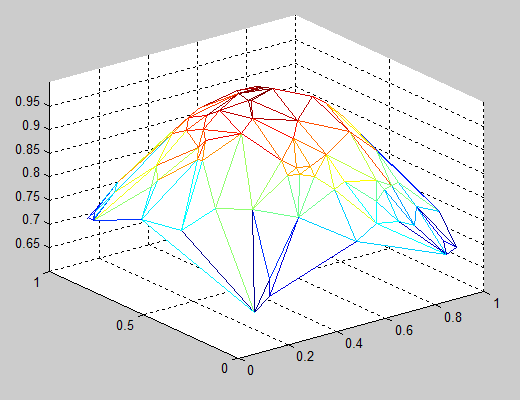
- Interpolate a regular mesh for your scattered points: You can use the TriScatteredInterp function to create an interpolant that you can evaluate at a given set of regularly spaced grid points, then plot the interpolated 3-D surface using the function MESH. Using the data from the example above:
[X,Y] = meshgrid(linspace(0,1,20)); % Create a regular grid F = TriScatteredInterp(x,y,z); % Create an interpolant Z = F(X,Y); % Evaluate the interpolant at the grid points mesh(X,Y,Z); % Plot the interpolated mesh
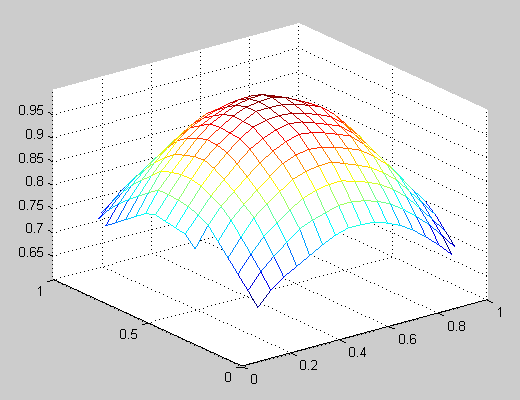
2 votes
1 vote
Categories
Find more on Data Import from MATLAB in Help Center and File Exchange
Products
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!