num2strexact (exact version of num2str)
num2strexact is a self-building C-mex function that converts a double or single input to the exact decimal string. The conversion is done with hundreds of digits of precision to maintain the exact conversion. The conversion uses the exact decimal value of each bit of the IEEE double precision floating point format along with the exact application of 2^exponent. Inf and NaN bit patterns are recognized, and denormalized numbers are handled also.
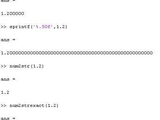
Don't confuse the exact conversion with significance! Double numbers will only be significant to about 15 decimal digits, and single numbers will only be significant to about 7 decimal digits. For example,
>> format hex
>> 1.2
ans =
3ff3333333333333
>> num2strexact(1.2)
ans =
1.1999999999999999555910790149937383830547332763671875
>> 1.2 + eps(1.2)
ans =
3ff3333333333334 <-- one bit different from 1.2
num2strexact(1.2 + eps(1.2))
ans =
1.20000000000000017763568394002504646778106689453125
>> num2strexact(eps(1.2))
ans =
2.220446049250313080847263336181640625e-16
You can see that 1.2 is not represented exactly in IEEE double format. The difference shows up in the 18th digit for this example. Then note that the very next number in the IEEE double format model is about 2e-16 bigger. The exact conversions are shown for each number, but they are not significant beyond the 16th digit shown. There are no numbers in between these two numbers that can be represented in IEEE double format.
Syntax:
Y = num2strexact(X [,'fixed' or 'float'])
[Y1 Y2] = num2strexact(X1,X2 [,'fixed' or 'float'])
[Y1 Y2 Y3] = num2strexact(X1,X2,X3 [,'fixed' or 'float'])
: :
etc etc
X = double or single or half
NOTE: The half type can be input in one of two ways:
1) A uint16 class variable containing the half bit patterns
2) A half class variable. num2strexact must have access to the
underlying bit patterns, so if you input a half class variable,
then this will first be converted to the equivalent integer bit
patterns with the storedInteger function (a temporary deep copy).
The number of inputs must match the number of outputs, except in the
special case of 1 input and 0 outputs where the result will simply be
put into ans. If the input is a scalar, the output will be a char string.
If the input is any other size array, the result will be a cell array of
the same dimensions as the input, with each cell containing the char
string conversion of the corresponding element.
The optional 'fixed' argument forces the result to be fixed point.
The optional 'float' argument forces the result to be floating point. All
numbers will be printed with exponents, even if the exponent is 0.
The default will be fixed or floating point depending on the size of the
decimal exponent. Numbers with -1 <= (decimal exponent) <= 2 will be
displayed as fixed point, else the number will be displayed as floating
point.
All NaN bit patterns, regardless of the sign bit and payload, will be
returned simply as the string 'NaN'.
Infinity bit patterns will be returned as 'Inf' or '-Inf' as appropriate.
num2strexact gives similar results to the following NUM2IEEE function by Steven Lord:
http://www.mathworks.com/matlabcentral/fileexchange/2996
except that num2strexact does not require the Symbolic Math Toolbox to display the potentially hundreds of exact digits, and num2strexact runs much faster.
Cite As
James Tursa (2025). num2strexact (exact version of num2str) (https://www.mathworks.com/matlabcentral/fileexchange/22239-num2strexact-exact-version-of-num2str), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Radar > Phased Array System Toolbox > Phased Array Design and Analysis > Antennas, Microphones, and Sonar Transducers >
Tags
Acknowledgements
Inspired: num2vpi - Converts input exactly into vpi, HPF - a big decimal class
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.