DFiltInt
DFiltInt designs interpolation filters that minimize the mean-square error for a signal with a given power spectral density. The program can be put to uses beyond just designing interpolation filters.
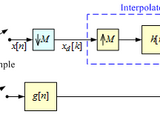
The interpolation filter under consideration is h[n] within the dashed lines (see figure). The filter design strategy minimizes the mean-square value of e[n]. The signal x(t) is a common input to both paths in the block diagram. This power spectrum of x(t) is used internally to calculate the correlation values needed. The lower reference path has an arbitrary delay τ, followed by a sampler, followed by a reference filter g[n].
The power spectrum of x(t) is modelled as the sum of a continuous spectrum and a discrete spectrum. The continuous-part is specified as a table of frequencies and power spectral density values for positive frequencies. The values in between the tabulated values are determined by a monotonic cubic interpolation.
The discrete part of the power spectrum models sinusoidal components in the input signal. These extra components can be used to give more weight to certain discrete frequencies. For instance adding a discrete component at zero frequency, will bias the solution to reproducing that frequency at the output of the interpolation filter more exactly. In the limit of a large dc discrete component, the interpolating filter will reproduce dc values with no error.
Features:
This program was originally based on the procedure described in paper by Oetken, Parks, and Schüssler [1]. That procedure was restricted to symmetric odd-length interpolating filters. The model power spectrum was flat. The present version of the program also draws inspiration from [2]. That paper suggests the addition of discrete components to the power spectrum to constrain the response at certain frequencies.
1. Flexible modelling of the power spectrum including both continuous and discrete components. The correlation functions are calculated from the interpolated tabulated values.
2. The provision for an arbitrary delay in the reference path. The provision for a given filter in the reference path. Special care taken to identify cases where the filter is symmetric or the error is zero at some phases.
Applications:
1. Interpolation Filter
The original application for the program was to design interpolation filters. In that application, g[n] is an identity filter (the default), and the delay τ is set to 〖(N〗_h-1)/2, where N_h is the number of coefficients in h[n]. The specified power spectrum serves as a weighting function – frequencies with a larger power spectrum affect the mean-square error more than regions with smaller values.
2. Fractional Delay Filter
If we set the interpolation factor to unity, we can design filters which approximate the delay in the reference path. This delay can be arbitrary. The power spectrum specification can be used as a frequency weighting to specify the range of frequencies for which the match should fit best.
3. Approximate a Reference Filter
We can use the program to approximate a response given by g[n]. For instance, g[n] can be a long response derived by truncating an IIR filter response after the response has decayed sufficiently. Then the filter h[n] will be an FIR filter which approximates the frequency response of g[n]. The power spectrum specification can be used as a frequency weighting to specify the range of frequencies for which the match should fit best.
Design Examples:
1. Interpolating Filter: Interpolation by a factor M=4, with a filter of length 22. The power spectrum is modelled as being constant up to 0.3Fs and then decreasing smoothly to zero at to 0.4Fs. The filter is coerced to have a response very close to M for dc inputs by adding a large discrete component to the power spectrum.
PSD.f = [0 0.3 0.4];
PSD.psd = [1 1 0];
PSD.fcos = 0;
PSD.Pcos = 10000;
M = 4;
h = DFiltInt (M, 22, PSD);
2. Fractional Delay Filter: This 24 coefficient filter will have a delay of 8.25 samples. We use the same continuous power spectrum as in the previous example. The group delay of the resulting filter will match the desired delay of 8.25 best at low frequencies.
PSD.f = [0 3 4];
PSD.psd = [1 1 0];
M = 1;
Delay = 8.25;
h = DFiltInt (M, 24, PSD, Delay);
1. G. Oetken, T. W. Parks and H. W. Schüssler, “New Results in the Design of Digital Interpolators”, IEEE Trans. Acoustics, Speech, Signal Processing, vol. 23, pp. 301–309, June 1975.
2. P. Kabal and E. Dubois, “Interpolating and Nyquist filters with Constraints at Certain Frequencies”, Signal Processing, vol. 24, no. 2, pp. 117–126, Aug. 1991(available on-line at http://www.ece.mcgill.ca/~pkabal/papers/).
Cite As
Peter Kabal (2025). DFiltInt (https://www.mathworks.com/matlabcentral/fileexchange/24666-dfiltint), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Signal Processing > Signal Processing Toolbox > Digital and Analog Filters > Digital Filter Design >
Tags
Communities
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
DFiltInt/
DFiltInt/private/
DFiltInt/private/test/
DFiltInt/test/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |