Fundamental Matrix Computation

This package, implements the 3 standard algorithms for the computation of the fundamental matrix.

Description

The implemented algorithms are:
1- The normalized 8 point algorithm
2- The algebraic error minimization(iterative)
3- The geometric error minimization(iterative)
and are the algorithms 11.1 to 11.3 of R. Hartley and A. Zisserman "Multiple View Geometry in Computer Vision".
The geometric error minimization includes the gold standard algorithm(MLE) as well as the Sampson approximation to the geometric error.
Usage of the code should be straightforward. The inputs and outputs to the functions, their dimensions and descriptions are available in the headers of each file. try help det_F_normalized_8point for example.
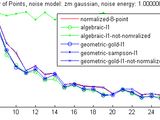
In order to be able to compare the performance of the algorithms, the same criterion as the book: the residual is used(see compare_results.m).
Also, different noise models are utilized to test the robustness of the algorithms: Gaussian additive noise, uniform noise and spurious noise(which can be seen as outliers).
To get the best results, it is possible to initialize the gold standard algorithm with the estimation of F computed from the algebraic minimization algorithm.

• Required Products: Optimization Toolbox
• MATLAB release: MATLAB 7.9 (2009b)

[Ran]

I'm trying to learn the field (3D view) and the software. I seem to miss the link between the fundamental matrix F and the camera matrices P1 and P2. It seems the "triangulate" function expects the camera matrices in canonical form (actually, only P2 since P1 is assumed [I|0]. Can you please elaborate on the process of getting P1 and P2 in canonical form from F? Perhaps add a function that does that?
As I said I'm new to this field so I hope I'm not making a fool of myself by asking this question…
Thanks,
Ran

[Omid Aghazadeh]

Hi Ran,
It seems that what you're looking for is a method to compute the Essential matrix. Fundamental matrix will allow uncalibrated reconstruction which would have a projective ambiguity. For a metric reconstruction with scale ambiguity, you will need calibrated cameras and the Essential matrix.
Hope it helped,
Omid

[km g]

the fundamental matrix is always changing or just a constant between two cameras?do i need to always choose few points for getting the fundamental matrix for different kind of image? sorry for any inconvenience.

[Omid Aghazadeh]

Fundamental matrix estimation is equivalent to estimating the image of the other camera in the other one; therefore if the view points of the cameras wrt eachother change, different fundamental matrices will describe the relation between the two cameras. See http://en.wikipedia.org/wiki/Epipolar_geometry.