ISEQUALFP: Check equality within floating point precision
ISEQUALFP Check two values for equality within floating point precision
It is widely known that floating point computation has a fundamental
limitation: not every value can be represented exactly. This can
lead to surprising results for those unfamiliar with this
limitation, especially since 'double' is MATLAB's default numerical
data type.
This function accepts two float values (single or double) or arrays
of floats, and returns a logical value indicating whether they
are equal within floating point precision. Mixed single and double
inputs will be evaluated based on single floating point precision.
Floating point accuracy reference:
http://blogs.mathworks.com/loren/2006/08/23/a-glimpse-into-floating-point-accuracy/
Usage:
yn = isequalfp(a,b)
a,b: floats or arrays of floats to compare
yn: logical scalar result indicating equality
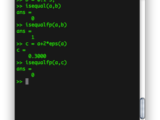
Example:
a = 0.3;
b = 0.1*3;
isequal(a,b) % ans = 0
isequalfp(a,b) % ans = 1
c = a+2*eps(a) % c = 0.3000...
isequalfp(a,c) % ans = 0
See also: EPS, ISEQUAL
Cite As
Andrew Davis (2024). ISEQUALFP: Check equality within floating point precision (https://www.mathworks.com/matlabcentral/fileexchange/36734-isequalfp-check-equality-within-floating-point-precision), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired: Solve Magic Square
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.