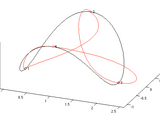
Smooth 3D bezier curves with implicit control points
Editor's Note: This file was selected as MATLAB Central Pick of the Week
This code can be used to draw 3D cubic splines by only entering the points through which the spline should pass.
In other words, smooth curves can be drawn by simply defining occasional points through which the curve should pass.
Bezier control points are calculated automatically using the Hobby's algorithm (1986), which allows a slope and "tension" of the spline at each point to be specified explicitly if desired.
Cite As
Will Robertson (2024). Smooth 3D bezier curves with implicit control points (https://www.mathworks.com/matlabcentral/fileexchange/42302-smooth-3d-bezier-curves-with-implicit-control-points), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |