Computing common zeros of two bivariate functions
r = rootsb(f,g,xydomain)
finds the common zeros of two bivariate functions f and g in the domain xydomain (4-element vector), which are given as function handles.
This code exists besides roots(f,g) in chebfun2 (which does essentially the same task) because it is sometimes better for accuracy to resample the functions when working in a subdivided, smaller domain.
If xydomain is not provided, it defaults to [-1 1 -1 1].
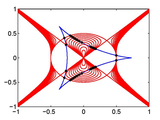
test.m runs a simple test and shows the plots of the solution along with the zero curves. The solutions should be the intersections of the curves.
This code always employs the algorithm based on the hidden variable resultant method. For the algorithmic details, see
[1] Y. Nakatsukasa, V. Noferini, and A. Townsend, Computing the common zeros of two bivariate functions via Bezout resultants, submitted (2013).
http://eprints.maths.ox.ac.uk/1704/
Cite As
Yuji Nakatsukasa (2025). Computing common zeros of two bivariate functions (https://www.mathworks.com/matlabcentral/fileexchange/44084-computing-common-zeros-of-two-bivariate-functions), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI and Statistics > Statistics and Machine Learning Toolbox > Cluster Analysis and Anomaly Detection > Nearest Neighbors >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |