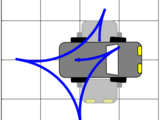
iLQG/DDP trajectory optimization
Solve the deterministic finite-horizon optimal control problem with the iLQG (iterative Linear Quadratic Gaussian) or modified DDP (Differential Dynamic Programming) algorithm. Includes two demos, a linear control-constrained problem and a car-parking problem. For details see
Tassa, Mansard and Todorov, 'Control-Limited Differential Dynamic Programming', ICRA 2014
Cite As
Yuval (2024). iLQG/DDP trajectory optimization (https://www.mathworks.com/matlabcentral/fileexchange/52069-ilqg-ddp-trajectory-optimization), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Control Systems > Control System Toolbox > Control System Design and Tuning > State-Space Control Design and Estimation >
Tags
Acknowledgements
Inspired: Belief Space Motion Planning using iLQG
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.