deleteOutliers2
[XOUT, YOUT, IDX, OUTLIERS] = DELETEOUTLIERS2(X, Y, F, C0, ALPHA, REP)
For input vectors x and y, returns vectors xOut, yOut with outliers
(at the significance level alpha) removed. The elements in vector x
specify data arguments and the elements in vector y the corresponding
data values. F is a function which is fit to the data y=F(x) in a least
square sense, where c0 is the initial function constants state for
fitting. Also, optional output argument idx returns the indices in
x and y of outlier values. Optional output argument outliers returns
the outlying values in y.
X is the input parameter. Default: 1:n where n = length(Y)
Y is the input data.
F is the function approximating the data distribution.
Default: Constant function.
C0 is the initial state of constants in function F.
ALPHA is the significance level for determination of outliers.
Default: Alpha = 0.05.
REP is an optional argument that forces the replacement of removed
elements with NaNs to presereve the length of X and Y.
This is an iterative implementation of the Grubbs Test that tests one
value at a time. In any given iteration, the tested value is either the
highest value, or the lowest, and is the value that is furthest
from the function approximation. Infinite elements are discarded if rep
is 0, or replaced with NaNs if rep is 1.
Appropriate application of the test requires that data can be reasonably
approximated by a normal distribution around the approximation function.
For reference, see:
1) "Procedures for Detecting Outlying Observations in Samples," by F.E.
Grubbs; Technometrics, 11-1:1--21; Feb., 1969, and
2) _Outliers in Statistical Data_, by V. Barnett and
T. Lewis; Wiley Series in Probability and Mathematical Statistics;
John Wiley & Sons; Chichester, 1994.
A good online discussion of the test is also given in NIST's Engineering
Statistics Handbook:
http://www.itl.nist.gov/div898/handbook/eda/section3/eda35h.htm
############ EXAMPLE - For full code see'testDeleteOutliers.m ###########
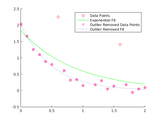
% define data points close to an exponential curve
x = 0:0.1:2;
y = 2*exp(-2*x) + randn(1,21)*0.1;
% exponential function definition
F = @(c,xdata)c(1)*exp(-c(2)*xdata);
c0 = [1 0]; % initial point
% delete outliers
[xOut,yOut,~,~] = deleteOutliers2(x, y, F, c0, 0.3, 0);
############################ END OF EXAMPLE #############################
Toolboxes required: Optimization Toolbox (function: lsqcurvefit)
Other m-files required: none
Subfunctions: zcritical
MAT-files required: none
See also: deleteoutliers, lsqcurvefit
Cite As
Christopher (2026). deleteOutliers2 (https://www.mathworks.com/matlabcentral/fileexchange/52827-deleteoutliers2), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired by: deleteoutliers
Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 | visualization added (plot created by testDeleteOutliers - script) |