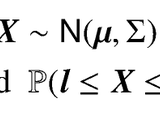Multivariate normal cumulative distribution
Version 1.1.0.0 (9.9 KB) by
Zdravko Botev
state-of-the-art algorithm for computing the multivariate normal cdf in high dimensions
Computes the probability Pr(l<X<u), where 'X' is a zero-mean multivariate normal vector with covariance 'Sig'.
In high dimensions, this algorithm is vastly superior to the one in Matlab's statistics toolbox, see example.
Reference: Z. I. Botev (2015), "The Normal Law Under Linear Restrictions: Simulation and Estimation via Minimax Tilting", submitted to JRSS(B)
Cite As
Zdravko Botev (2026). Multivariate normal cumulative distribution (https://www.mathworks.com/matlabcentral/fileexchange/53583-multivariate-normal-cumulative-distribution), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Created with
R2015b
Compatible with any release
Platform Compatibility
Windows macOS LinuxCategories
- AI and Statistics > Statistics and Machine Learning Toolbox > Probability Distributions and Hypothesis Tests > Multivariate Distributions > Multivariate Normal Distribution >
Find more on Multivariate Normal Distribution in Help Center and MATLAB Answers
Tags
Acknowledgements
Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.