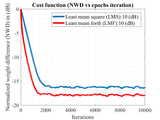
System Identification Using Least Mean Forth (LMF) and Least Mean Square (LMS) algorithm
In this simulation least mean square (LMS) and least mean forth (LMF) algorithms are compared in non-Gaussian noisy environment for system identification task. Is it well known that the LMF algorithm outperforms the LMS algorithm in non-Gaussian environment, the same results can be seen in this implementation. Additionally a customized function for additive white uniform noise is also programmed.
Cite As
Shujaat Khan (2021). System Identification Using Least Mean Forth (LMF) and Least Mean Square (LMS) algorithm (https://www.mathworks.com/matlabcentral/fileexchange/63596-system-identification-using-least-mean-forth-lmf-and-least-mean-square-lms-algorithm), MATLAB Central File Exchange. Retrieved .
Comments and Ratings (5)
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired by: Add white Uniform noise to a signal, System Identification Using Recursive Least Square (RLS) and Least Mean Square (LMS) algorithm
Inspired: Variable Step-Size Least Mean Square (VSS-LMS) Algorithm
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Plant_Identification_LMS_LMF/
Plant_Identification_LMS_LMF/html/
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
Select web siteYou can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
When I use the Algorithm in a complex system where the input and the output are complex. I didn't get the expected results/curves. Does the command need to be modified adapted to the complex values?
Sir can you please suggest some papers on blind system identification in time varying system
Thank you @jing zhang and @Rui Yang