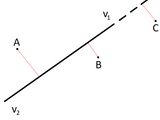
point to line distance
calculate the distance between a 2D or 3D line and one or more points
You are now following this Submission
- You will see updates in your followed content feed
- You may receive emails, depending on your communication preferences
You can input either a 2D or a 3D line and 2D or 3D points. This function is an extended version of the line below, with some input checking:
distance=norm(cross(v1-v2,pt-v2))/norm(v1-v2)
Licence: CC by-nc-sa 4.0
Cite As
Rik (2026). point to line distance (https://github.com/thrynae/point_to_line_distance/releases/tag/1.3.2), GitHub. Retrieved .
General Information
- Version 1.3.2 (3.52 KB)
-
View License on GitHub
MATLAB Release Compatibility
- Compatible with R13SP1 and later releases
Platform Compatibility
- Windows
- macOS
- Linux
| Version | Published | Release Notes | Action |
|---|---|---|---|
| 1.3.2 | See release notes for this release on GitHub: https://github.com/thrynae/point_to_line_distance/releases/tag/1.3.2 |
||
| 1.3.1 | added tester and example file, and added logo |
||
| 1.3.0.0 | fixed issue with 2D input |
||
| 1.2.0.0 | added compatibility for R13 (MATLAB 6.5) |
||
| 1.1.0.0 | uploaded incorrect version, so now a bug in the orientation is fixed |
||
| 1.0.0.0 |
To view or report issues in this GitHub add-on, visit the GitHub Repository.
To view or report issues in this GitHub add-on, visit the GitHub Repository.
