simpleICP

Implementations of a rather simple version of the Iterative Closest Point algorithm in various languages.

simpleICP

This repo contains implementations of a rather simple version of the Iterative Closest Point (ICP) algorithm in various languages.

Currently, an implementation is available for:

Language	Code	Main dependencies
C++	Link	nanoflann, Eigen, cxxopts
Julia	Link	NearestNeighbors.jl
Matlab	Link	Statistics and Machine Learning Toolbox
Octave	Link
Python	Link	NumPy, SciPy

I've tried to optimize the readability of the code, i.e. the code structure is as simple as possible and tests are rather rare.

The C++ version can be used through a cli interface.

Also available at:

• Matlab:
• Python:

Features of the ICP algorithm

Basic features

The following basic features are implemented in all languages:

• Usage of the signed point-to-plane distance (instead of the point-to-point distance) as error metric. Main reasons:
  • higher convergence speed, see e.g. here and here
  • better final point cloud alignment (under the assumption that both point clouds are differently sampled, i.e. no real point-to-point correspondences exist)
• Estimation of a rigid-body transformation (rotation + translation) for the movable point cloud. The final transformation is given as homogeneous transformation matrix H:

  H = [R(0,0) R(0,1) R(0,2)   tx]
      [R(1,0) R(1,1) R(1,2)   ty]
      [R(2,0) R(2,1) R(2,2)   tz]
      [     0      0      0    1]
  

  where R is the rotation matrix and tx, ty, and tz are the components of the translation vector. Using H, the movable point cloud can be transformed with:

  Xt = H*X
  

  where X is a 4-by-n matrix holding in each column the homogeneous coordinates x, y, z, 1 of a single point, and Xt is the resulting 4-by-n matrix with the transformed points.
• Selection of a fixed number of correspondences between the fixed and the movable point cloud. Default is correspondences = 1000.
• Automatic rejection of potentially wrong correspondences on the basis of
  1. the median of absolute deviations. A correspondence i is rejected if |dist_i-median(dists)| > 3*sig_mad, where sig_mad = 1.4826*mad(dists).
  2. the planarity of the plane used to estimate the normal vector (see below). The planarity is defined as P = (ev2-ev3)/ev1 (ev1 >= ev2 >= ev3), where ev are the eigenvalues of the covariance matrix of the points used to estimate the normal vector. A correspondence i is rejected if P_i < min_planarity. Default is min_planarity = 0.3.
• After each iteration a convergence criteria is tested: if the mean and the standard deviation of the point-to-plane distances do not change more than min_change percent, the iteration is stopped. Default is min_change = 1.
• The normal vector of the plane (needed to compute the point-to-plane distance) is estimated from the fixed point cloud using a fixed number of neighbors. Default is neighbors = 10.
• The point clouds must not fully overlap, i.e. a partial overlap of the point cloud is allowed. An example for such a case is the Bunny dataset, see here. The initial overlapping area between two point clouds can be defined by the parameter max_overlap_distance. More specifically, the correspondences are only selected across points of the fixed point cloud for which the initial distance to the nearest neighbor of the movable point cloud is <= max_overlap_distance.

Output

All implementations generate the same screen output. This is an example from the C++ version for the Bunny dataset:

$ run_simpleicp.sh
Processing dataset "Bunny"
[09:42:37.690] Create point cloud objects ...
[09:42:37.690] Consider partial overlap of point clouds ...
[09:42:37.770] Select points for correspondences within overlap area of fixed point cloud ...
[09:42:37.770] Estimate normals of selected points ...
[09:42:37.775] Start iterations ...
[09:42:37.780] Iteration | correspondences | mean(residuals) |  std(residuals)
[09:42:37.780]         0 |             960 |         -0.0003 |          0.0025
[09:42:37.780]         1 |             960 |          0.0000 |          0.0013
[09:42:37.785]         2 |             903 |         -0.0000 |          0.0005
[09:42:37.790]         3 |             903 |         -0.0000 |          0.0004
[09:42:37.794]         4 |             883 |         -0.0000 |          0.0003
[09:42:37.799]         5 |             877 |         -0.0000 |          0.0003
[09:42:37.803]         6 |             869 |         -0.0000 |          0.0002
[09:42:37.808]         7 |             860 |         -0.0000 |          0.0002
[09:42:37.813]         8 |             855 |         -0.0000 |          0.0002
[09:42:37.818]         9 |             851 |         -0.0000 |          0.0002
[09:42:37.822]        10 |             849 |         -0.0000 |          0.0002
[09:42:37.827] Convergence criteria fulfilled -> stop iteration!
[09:42:37.827] Estimated transformation matrix H:
[09:42:37.827] [    0.990045    -0.172046     0.000965    -0.000304]
[09:42:37.827] [    0.172037     0.990039    -0.001838    -0.000220]
[09:42:37.827] [   -0.000824     0.001815     1.000023    -0.000015]
[09:42:37.827] [    0.000000     0.000000     0.000000     1.000000]
[09:42:37.827] Finished in 0.137 seconds!

Test data sets

The test data sets are included in the data subfolder. An example call for each language can be found in the run_simpleicp.* files, e.g. run_simpleicp.py for the python version.

Dataset		pc1 (no_pts)	pc2 (no_pts)	Overlap	Source
Dragon		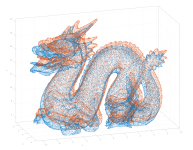pc1 (100k)	pc2 (100k)	full overlap	The Stanford 3D Scanning Repository
Airborne Lidar		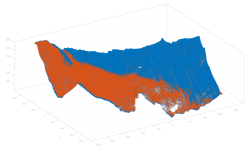pc1 (1340k)	pc2 (1340k)	full overlap	Airborne Lidar fligth campaign over Austrian Alps
Terrestrial Lidar		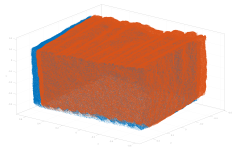pc1 (1250k)	pc2 (1250k)	full overlap	Terrestrial Lidar point clouds of a stone block
Bunny		pc1 (21k)	pc2 (22k)	partial overlap	The Stanford 3D Scanning Repository

Benchmark

These are the runtimes on my PC for the data sets above:

Dataset	C++	Julia	Matlab	Octave*	Python
Dragon	0.16s	3.99s	1.34s	95.7s	0.89s
Airborne Lidar	3.98s	5.38s	15.08s	-	5.45s
Terrestrial Lidar	3.62s	5.22s	13.24s	-	5.68s
Bunny	0.13s	0.38s	0.37s	72.8s	0.80s

For all versions the same input parameters (correspondences, neighbors, ...) are used.

* Unfortunately, I haven't found an implementation of a kd tree in Octave (it is not yet implemented in the Statistics package). Thus, a (very time-consuming!) exhaustive nearest neighbor search is used instead. For larger datasets the Octave timings are missing, as the distance matrix does not fit into memory.

References

Please cite related papers if you use this code:

@article{glira2015a,
  title={A Correspondence Framework for ALS Strip Adjustments based on Variants of the ICP Algorithm},
  author={Glira, Philipp and Pfeifer, Norbert and Briese, Christian and Ressl, Camillo},
  journal={Photogrammetrie-Fernerkundung-Geoinformation},
  volume={2015},
  number={4},
  pages={275--289},
  year={2015},
  publisher={E. Schweizerbart'sche Verlagsbuchhandlung}
}

Related projects

• globalICP: A multi-scan ICP implementation for Matlab