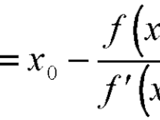Newton's Forward Interpolation

Matlab codes for Newton's Forward Interpolation.

Newton's Interpolation

Script for Newton's Interpolation formula.

Script for Newton's Interpolationnewton_interpolation(x, y, p)x and y are two Row Matrices and p is point of interpolationExample>> x=[1,2,4,7,8]>> y=[-9,-41,-189,9,523]>&gt

GUI Numerical Solver

GUI Numerical Solver including curve fitting, root finding and linear system solver using most of the popular methods.

Numerical Solver includes the following :- Roots Finding -> Bisection -> False-Position -> Simple Fixed Point -> Newton-Raphson Method (Multivariable

Newton interpolation coefficient

This function finds the coefficients for Newton interpolation polynomial

% [b0 b1 b2...] = NewtonInterpolation(x,y) where vector [b0 b1 b2...] is% the coefficients of Newton interpolation polynomial:% % N(x) = b0+b1(x-x0)+b2(x-x0)(x-x1)+...% % Note that both x, y

Newton's Backward Interpolation

Matlab codes for Newton's Backward Interpolation.

Newton Backward interpolation

Newton Backward interpolation

Code for Newton Backward interpolation::::: Newton Backward interpolation ::::::Enter x : [0.01 0.02 0.03 0.04 0.05]Enter y : [98.434 48.439 31.778 23.449 18.454]Enter point to consider : 0.045F =

Newton Forward Interpolation

Interpolation by Newton Forward

This is code for Newton forward interpolation::::: Newton Forward interpolation ::::::Enter x : [75 80 85 90]Enter y : [246 202 118 40]Enter point to consider : 79F = 246 0 0 0 202

Newton's Polynomial Interpolation

Interpolates a scalar or vector yp = f(xp) with given x and y = f(x) vectors and xp query

Newton's Polynomial Interpolation based on Taylor's Series and finite differences.Example data:x = [1 4 6 5]; % x vectory = log(x); % y = f(x) vectorxp = 2 or xp = [2 3]; % x point(s) (scalar or

Newton’s Divided Difference Interpolation

Matlab codes for Newton’s Divided Difference Interpolation

Interpolation Newton - function generator

Code Help Students

practical and educational - simpleReference:https://www.mathworks.com/matlabcentral/fileexchange/7405-newton-s-interpolation?focused=5061850&tab=function

newton2poly

newton2poly generates the polynomial formula given newton interpolation coefficients and x-coordinate interpolation nodes.

newton2poly generates the polynomial formula given newton interpolation coefficients and x-coordinate interpolation nodes as:p(x) = c(1) + c(2)*(x-nodes(1)) + c(3)*(x-nodes(1))*(x-nodes(2))...INPUT:c

Numerical Interpolation Methods for MATLAB

Matlab codes for numerical Interpolations: Newton’s Forward, Newton’s Backward, Divide difference, Lagrange’s Interpolation. Video lecture.

all interpolation method

symbolic equation of all interpolation method include lagrange ,newton ,forward and backward.

this file include all interpolation method :lagrange method newton method forward_differences backward_differencesyou can find the polynomial equation and the solutions of each of them easily .

3D Data Interpolation

3D interpolation using modified 4-point vector Newton interpolation

Syntax: ui=NewtFit(x,y,z,u,xi,yi,zi)3D interpolation. It may be used where griddata3 fails to find a triangularization of the datagrid (x,y,z). The function uses a modified 4 point Newton

Regular Control Point Interpolation Matrix with Boundary Conditions

Creates Toeplitz-like matrices representing interpolation operations with edge conditions.

The main file interpMatrix.m in this package creates a sparse Toeplitz-like matrix representing a regularly-spaced interpolation operation between a set of control points. The user can specify the

Numerical Interpolation & Differentiation

Interpolate and Differentiate numerical datasets by generating a function for equal interval using Newton Forward/Backward & Sterling Method

program utilizes Newton's Forward/Backward Difference and Stirling's method for this purpose, which requires that the interval of the independent variable remains consistent across the dataset.Here's a

interparc

Distance based interpolation along a general curve in space

spaced, others not so close, and they wish to create a new set which is uniformly spaced along the same curve.When the interpolation is assumed to be piecewise linear, this is easy. However, if the curve

Fast Linear Interpolation

Performs linear interpolation with a speed acceleration of (up to) 4x.

F = lininterp1f(X,Y,XI,Ydefault) returns the value of the 1-D function Y at the points XI using linear interpolation. Length(F)=length(XI). The vector X specifies the coordinates of the underlying

Fast interpolation

Performs nearest-neighbor or linear interpolation much faster than interp1 when an evenly-spaced lib

This function performs interpolation faster than MATLAB's "interp1" function. In the limit of small library and search arrays, it is ~5x faster. In the limit of large library arrays, qinterp1 has a

Newton-Raphson method

Newton-Raphson is a root-finding algorithm which produces successively better approximations to the roots of a real-valued function.

The Newton-Raphson method (also known as Newton's method) is a way to quickly find a good approximation for the root of a real-valued function f(x)=0. It uses the idea that a continuous and

Lagrange's Interpolation

Matlab codes for Lagrange's Interpolation. The detailed method and codes are available in the video lecture given in the description.

S6&7_AN

The Lagrange interpolation The Newton's Divided Difference Interpolation

hermitePoly

The function returns Hermite interpolation polynomomial from given data.

and function values are given, the polynomial is similar to Newton interpolation polynomial.

Newton-Raphson Loadflow

These matlab m files are used to calculate bus voltages and angles using Newton Raphson iterative me

These matlab m files are used to calculate bus voltages and angles, power flows using Newton Raphson iterative method

Newton's Method

Newton's method for finding zeros of a function.

Newton's method for finding successively better approximations to the zeroes of a real-valued function.

Lagrange polynomial interpolation

Lagrange polynomial interpolation

Approx a point-defined function using Lagrange polinomial interpolation method

The Newton - Raphson Method

The Script Provides a demonstration of the "Newton - Raphson Method" , to solve various polynomial and transcendental equations

"The Newton - Raphson Method" uses one initial approximation to solve a given equation y = f(x).In this method the function f(x) , is approximated by a tangent line, whose equation is found from the

Interpolation Utilities

A variety of 1-D interpolation utilities

This zip file contains functions related to 1-D interpolation:1) analyticint.m performs piecewise analytic interpolation2) baryinv.m performs barycentric interpolation with inverse distance

Newton's Method

Newton's Method to find the roots of a polynomial

This function can be used to perform Newton-Raphson method to detect the root of a polynomial. It starts from an initial guess by user and iterates until satisfy the required convergence criterion

Newton's Method Animation

Uses Newton's method to calculate a root to a polynomial function.

Calculates the root to a polynomial function using Newton's method. The root at each iteration is plotted against the graph of the original function. Feel free to try different functions (plotting

Newton form for interpolating polynomials

newton_interpolation.m provides a simple tool for interpolating any function.

It gets any equation and the degree of the its interpolating polynomial as well as the interpolation interval and returns the symbolic newton form of the polynomial. For educational purposes, the

peakfinder(x0, sel, thresh, extrema, includeEndpoints, interpolate)

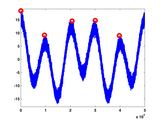
Quickly finds local maxima (peaks) or minima (valleys) in a noisy signal.

Newton interpolation polynomial

Obtains an interpolating polynomial for the form of Newton

Dynamic program with good user-machine communication, allows inverse and direct interpolations and displays an interpolated polynomial over any number of points.

Newton-Raphson

Newton-Raphson method for all real roots of the polynomial.

Faster linear Interpolation

Much faster version of the interp functions, but ONLY for LINEAR interpolation

Matlab code for Lagrange interpolation

Lagrange interpolation

N-dimensional Fourier interpolation

Performs N-D FFT interpolation with upsampling, downsampling, or mixed up- and downsampling

Performs N-D FFT interpolation on any data for which fftn works. Will upsample by zero-filling, downsample by truncating high frequencies, or combine both up- and downsampling by dimension to allow

Lagrange Interpolation

Simple MATLAB file for Lagrange Interpolation

Scattered Data Interpolation and Approximation using Radial Base Functions

Set of functions that can be used for interpolation and and approximation of scattered data of any d

Radial base functions (RBF) can be used for interpolation and and approximation of scattered data i.e. data is not required to be on any regular grid. The same function can handle data interpolation

Newton's Method for Divided Differences.

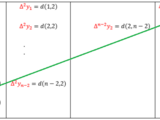
Newton's Method for Divided Differences.

Newton's Method for Divided Differences.The following formula is solved:Pn(x) = f(x0) + f[x0,x1](x-x0) + f[x0,x1,x2](x-x0)(x-x1) + ... + f[x0,x1,..,xn](x-x0)(x-x1)..(x-x[n-1])Where:f[x0,x1] =

Non-linear equations system solver (Newton Raphson)

Solves a non-linear system with iterative Newton-Raphson. Very easy and powerfull!!

Newton fractal

Function for generating Newton fractal.

Very simple function that can generate 12 different type of Newton fractal. newtonFractalRGB.m can generate RGB images.

Quadratic Interpolation Optimization (QIO)

Quadratic Interpolation Optimization (QIO): a new mathematics-based metaheuristic algorithm for global optimization

Quadratic Interpolation Optimization (QIO) is a new optimization approach for solving optimization problems. QIO is motivated derived from mathematics, specifically the newly proposed generalized

Transfinite Interpolation

To demonstrate grid generation using Transfinite Interpolation

is by interpolation. Grid generation based on interpolation has two basic advantages;rapid computation of grids anddirect control over grid point locationsThese advantages are offset by the fact that

sifReader - Read Andor Newton .sif files into matlab.

Read sif files generated by an Andor Newton camera into matlab.

to modify his code to be able to read in sif files generated with our setup (Andor Newton EMCCD + Solis 4.16). This package also contains an important adjustment to Leutenagger's. We found

Fast 2-dimensional interpolation

Provides a 5x-50x speedup over interp2

This function performs 2-dimensional interpolation similar to MATLAB's built-in function interp2 with a considerable speed advantage.qinterp2 may only be used with evenly-spaced, monotonically

Newton's Divided Differences and its associated Polynomial

Computes Newton's table for Divided Differences and the coefficients of the associated polynomial function for a given dataset (X,Y).

capability of directly outputting the coefficients of the associated polynomial. So that the polynomial can be evaluated to produce interpolations/extrapolations directly with Matlab's 'polyval' function.Happy

Newton-Raphson Method for a nonlinear System of 3 variables

The function returns the solution of three equations in three variables using the Newton-Raphson method.

The function returns the solution of three equations in three variables using the Newton-Raphson method. The inputs are symbolic functions, initial guesses and number of iterations.Here's an

Periodical Cubic Interpolation

PERIODICAL PIECEWISE CUBIC HERMITE INTERPOLATING POLYNOMIAL: THE FUNCTIONS PERPCHIP AND PERSPLINE

NewtonRaphson.m

Newton Raphson Method Example

Robust Newton Raphson Method example, This can be changed to fit most forms.

NewtonRaphson

Yet another solver that uses the backslash function to solve a set of non-linear equations

Although this is the most basic non-linear solver, it is surprisingly powerful. It is based on the Newton-Raphson method in chapter 9.6-7 of Numerical Recipes in C. In general for well behaved

Newton-Raphson Method

Newton-Raphson Method to find Real Root of Functions

The Newton-Raphson Method is a better version of the Fixed Point Interation Method, increasing the speed of the convergence to find the root of the equation. The NRM uses divisions, so it can give a

Newton-Raphson Method for 2 variables

Newton method for non-linear system of 2 variables (also solves linear system)

This program calculates the roots of a system of non-linear equations in 2 variables. This a script file and you only have to write in the command windows ">>newton2v2", and the program ask

Mesh Laplacian Interpolation Operator

Computes the zero Laplacian interpolation matrix

See also MESH_LAPLACIAN function on matlab central file exchange.MESH_LAPLACIAN_INTERP: Computes the zero Laplacian interpolation matrix Useage: [int, keepindex, repindex] =

Newton Raphson Method

A simple Matlab Code for Newton Raphson Method

A simple Matlab code for solving newton Raphson method numerically.

2D interpolation

Fast 2D linear interpolation of scalar of vector valued 2D images.

INTERP2(Z(:,:,3),XI,YI); The extra speed gain is from the precomputation of coefficients for interpolation, which are the same for all images. Interpolation of a set of images is useful, e.g. for image registration, when

Time-domain Sinc Interpolation (Resampling)

Time-domain SINC resampling (interpolation) function with a simple example

A robust interpolation function using a SINC kernel to convolve the original input time series in order to get resampled time series. A simple example is provided in comment section to illustrate how

ScaleTime

Fast linear interpolation of equally spaced data (C-MEX and M)

ScaleTime - fast linear matrix interpolation Yi = ScaleTime(Y, T)Where T is a vector with values between 1 and size(Y,1). This is equivalent to Yi = interp1(1:size(Y, 1), Y, T, 'linear')If T is

Generalized Newton Raphson Method

Newton Raphson Method for any number of variables and any number of equations

Two methods are provided - 1) an automatic updation method which can be effectively used outside of a loop since it writes out a newton-raphson computation file from the parameters received.2) a

Newton Raphson Method

Root Finding Method (Newton Raphson)