34,291 results
Draw, manipulate and reconstruct B-splines.
estimate B-splines with known knot vector, given a set of noisy data points either with known or unknown associated parameter values.As regards the interactive interface, the user is shown a figure window
B-spline registration of two 2D / 3D images or corrsp. points, affine and with smooth b-spline grid.
Affine and B-spline grid based registration and data-fitting of two 2D color/grayscale images or 3D volumes or point-data. Registration can be done intensity / pixel based, or landmark /
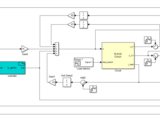
A non-local learning rule is employed in a repetitive neurocontroller based on B-spline network.
http://dx.doi.org/10.1109/IECON.2013.6700120 [**] weight constraints are used instead of forgetting and that turns out to robustify the controller. Hence, the same idea has been tested also in the B-spline based repetitive neurocontroller
MATLAB library for elastic functional data analysis
Using Implicit B-Splines for Surface Reconstruction out of 3D point clouds.
Using Implicit B-Splines for Surface Reconstruction out of 3D point clouds.Please cite the following paper, in case of using the code:Rouhani M. and Sappa A.D., Implicit B-spline fitting using the 3L
Fit, evaluate, differentiate non-uniform B-splines of any order - fast
fastBSpline - A fast, lightweight class that implements non-uniform B splines of any order Matlab's spline functions are very general. This generality comes at the price of speed. For large-scale
Numerical computation with functions
Finite element library for solving plane elasticity problems
A toolbox for nonparametric probability function estimation using normalized B-splines
A MATLAB toolbox 'bsspdfest' implementing nonparametric probability function estimation using normalized B-splines was developed. The toolbox implements nonparametric probability function estimation
Computes the B-spline approximation from a set of coordinates. Supports periodicity and n-th order approximation.
Computes the B-spline approximation from a set of coordinates (knots).The number of points per interval (default: 10) and the order of the B-spline (default: 3) can be changed. Periodic boundaries
Shape Context based nonrigid registration of 2D/3D objects, to build Active Shape Models
Shape Context is a method to get an unique descriptor (feature vector) for every point of an object contour or surface. This descriptor is used in combination with a b-spline free form deformation
Basic toolbox for polynomial B-splines on a uniform grid. OO overloading of common operators.
B-splines is a natural signal representation for continous signals, wheremany continous-domain operations can be carried out exactly once theB-spline approximation has been done.The B-spline
Complete Matlab pipeline for large scale calcium imaging data analysis
Spline toolbox for the definition, evaluation and visualization of spline curves and surfaces based on standard B-splines
The Spline toolbox allows the definition, evaluation and visualization of spline curves and surfaces based on standard B-splines. Furthermore, it provides an approximation algorithm with the
Given a 3D cloud of points accompanied by normals an implicit b-spline surface is reconstructed.
A fast surface reconstruction is implemented in this set of codes. Given a 3D cloud of points accompanied by normal vectors an implicit b-spline surface will be reconstructed.Please cite the
Converted NURBS toolbox
Creates Toeplitz-like matrices representing interpolation operations with edge conditions.
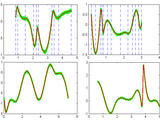
reconstruction using cubic B-splines with different possible boundary conditions. The screenshot above shows the output of this example, and illustrates how improved signal reconstruction is obtained using
B-splines interpolation
Interpolación por basic splines. Para apoyo en las clases de creación de videojuegos de la Universidad Loyola, en Sevilla.
A toolbox for performing image registrations on 4D RTOG files or any other volumetric image.
This toolbox contains all the functions necessary for extraction and registration of medical RTOG images using a cubic-B-spline free form deformation technique. The optimization routine uses a
Separating periodic signals from their aperiodic background
presents a method for modelling periodic signals having an aperiodic trend using the method of variable projection. In particular, this paper focuses on using B-Splines to model the a-periodic portion. The
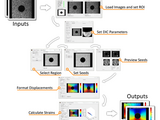
2D-DIC program that uses contiguous circular subsets, biquintic B-spline interp, and complex ROIs
Basis functions for B-Splines (including nonrational and rational B-Splines).
Given the number of control points(N), the order of Splines (K), a sequence of knot vector (T), and the file name of txt format, the function basisfunc_NBS computes the nonrational (unweighted) basis
This computes the H-infinity optimal causal filter (indirect B-spline filter) for the cubic spline.
Computes the H-infinity optimal causal filter (indirect B-spline filter) for the cubic spline.[INPUT]d: delay[OUTPUT]psi: the optimal filter psi(z) in a TF objectgopt: optimal valueThis file is based
Some basic codes in Computer Aided Design
Surface16.Plot B-Spline Curve
Workflow for chromatogram alignment using the semi-parametric time warping algorithm
Version 1.0.0.0
Christina de Bruyn KopsWorkflow for chromatogram alignment using the semi-parametric time warping algorithm
Least squares approximation of 1D data using free-knots spline
The purpose of this function is to provide a flexible and robust fit to one-dimensional data using free-knot splines. The knots are free and able to cope with rapid change in the underlying model
Construct coefficients of interpolating or smoothing BSplines from N-dimensional array, analytically
Class to enable BSpline signal and image processing. Based off of the papers:M. Unser, A. Aldroubi, and M. Eden, "B-Spline Signal Processing: Part I - Theory," IEEE Trans Sig Proc, 41(2):821-833
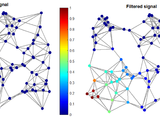
Signal Processing on non-euclidien domain signals
AxonSeg is a GUI that performs axon and myelin segmentation on histology images.
A recursive function that computes the b-spline basis atoms, it's very compact
a function to compute the b-spline points on a gridusage y = spline_recursion (u,n)n is the order of the spline u is the grid pointexample:t=linspace(-2,10,10000);y1=spline
nu_corrector is a tool for correcting vignetting and bias of image.
with an MRI machine, or by non-uniform X-ray beam for CT images acquired with a CT scanner. Bias is a smooth field in any format, which can be represented by for example a bipoly model, B-Spline
Spline object modification / transformation
A little piece of code enabling quick modification of spline objects: clipping, shifting, and scaling in both x, and y.
Zero-phase filtering using B-Spline networks.
bsn1.m implements a zerophase low pass filter using a novel structure called B-Spline Networks (BSN).This function was originally developed for use with the LFFC (learning feedforward control).A nice
Matlab codes for first generation curvelet and ridgelet transforms.
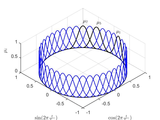
The concept of B-spline based repetitive control is explored within the frame of motion control.
remember to click the Build button in the S-Function block before attempting to run the model. More info: M. Malkowski, B. Ufnalski and L. M. Grzesiak, B-spline based repetitive controller revisited: error
Planar Cosserat rod
Zero-phase filtering using B-Spline Networks with dilation 2.
Similar to "bsn1.m", "bsn2.m" provides dilation 2 in the B-Spline network (BSN) which are used as a new way of performing approximate zero-phase low pass filtering.The transfer function of the
Draw Cubic, Hermite, Bezier and B-Spline curves by entered points.
This software package creates subdivision matrices for generalized quadratic and cubic B-spline subdivision surfaces and volumes.
# A-New-Approach-to-the-Construction-of-Subdivision-Algorithms-The-MATLAB-Software-PackageThis software package creates subdivision matrices for generalized quadratic and cubic B-spline subdivision
Model and scripts from video series on Simcape physical modeling
MATLAB interface to aid in plotting of VMEC output.
A folder containing essential MATLAB functions that are not included in the standard distribution.
Personalized Statistical Modeling of Soft Tissue Structures in the Knee. Generative code
Core tools required for running Canlab Matlab toolboxes. The heart of this toolbox is object-oriented tools that enable interactive analysis
A toolbox for medical image registration.
Toolbox in MATLAB for modelling of overhead and underground transmission lines.
Lay Data
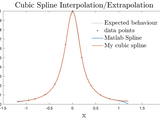
A vectorized, parallel capable, cubic spline interpolation/extrapolation function for non-uniformly distributed 1d data
The publication of this function was inspired by the poor job done by several implementations of the 1d cubic spline publications in Matlab's file exchange repos.This function was part of one of my
RRT, RRT*, RRT*FN algorithms for MATLAB
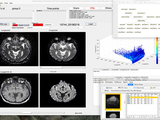
Medical software for Processing multi-Parametric images Pipelines
requirements:Matlab 2017b or higherToolboxes (Mandatory : Image Processing Toolbox -- Recommended : Statistics and Machine Learning Toolbox ; Parallel Computing Toolbox)Java 8 or higherData to process in Bruker / DICOM
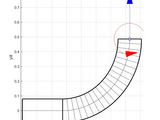
Fits two points with assigned directions with a single clothoid curve
A Matlab toolbox for cardiovascular signal processing
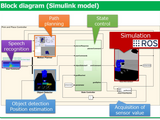
Pick & Place application by integrating Matlab & ROS
Flexible Algorithms for Image Registration
This is an image registration Matlab program developed based on B-spline composition and level sets.
In this code, the image is defined using B-spline level set functions and they are deformed by using a composition approach. The computation composed of efficient algorithms for calculating the
C-code version of B-spline repetitive controller
This model is a C-code version of http://www.mathworks.com/matlabcentral/fileexchange/49023-b-spline-based-repetitive-neurocontroller uploaded by Bartlomiej Ufnalski.
The program splineLength.m calculates numerically the arc length of an arbitrary B-splines.
The program splineLength.m calculates numerically the arc length of an arbitrary B-spline. Numerical integration uses "waypoints" for high precision.
Calculates Sound Power and Analyzes Source Directivity from Sound Pressure on spherical coordinates.
Encrypt B-Spline Curves and Surfaces using chaotic systems
The code implements the B-Spline curve and surface encryption method proposed in the following work:Moysis, L., Lawnik, M., Antoniades, I. P., Kafetzis, I., Baptista, M. S., & Volos, C. (2023