Understanding Field-Oriented Control | Motor Control, Part 4
From the series: Motor Control
Melda Ulusoy, MathWorks
Field-oriented control (FOC) is a technique used to control various motor types, including permanent magnet synchronous machines (PMSMs). FOC makes use of Clarke and Park transforms that convert the three-phase sinusoidal currents into the direct and quadrature currents. You’ll learn how the direct and quadrature currents are controlled to bring the stator field vector orthogonal to the rotor field vector to maximize the generated torque.
Published: 26 Apr 2020
In this video, we’re going to talk about field-oriented control, which is also referred to as FOC. We’ll discuss why we use FOC and the Clarke and Park transforms that are required to implement an FOC algorithm.
In the previous videos, we discussed how BLDC motors work and how we spin them using six-step commutation or trapezoidal control. One of the drawbacks with this type of control are the ripples that we observe in the speed and torque responses of the motor. Here, the cyan and magenta vectors show us how the magnitude and direction of the rotor and stator magnetic fields change during six-step commutation of a BLDC motor. We clearly see that the angle between the stator and rotor magnetic fields fluctuates between 60 and 120 degrees. This is the reason behind the speed and torque ripples. It also prevents us from getting the maximum torque, which occurs when the fields align at 90 degrees.
We overcome the shortcomings of the six-step commutation with field-oriented control on PMSM motors. Here’s another animation that shows us the resulting rotor and stator magnetic fields when we implement field-oriented control on a PMSM motor. You see how the stator field direction stays always orthogonal to the rotor field. Field-oriented control greatly reduces the ripples of the system response and leads to smoother operation of the motor. It also allows the motor to run at speeds higher than the nominal speed using a technique called field weakening. One thing to note here is that you get these benefits at the cost of implementing a more complex control algorithm than the six-step commutation. Because now instead of DC currents, you’re dealing with AC signals to control the motor.
Next, we’ll talk about how the FOC algorithm works. Let’s say we want to control a PMSM motor using FOC. Our goal here is to produce torque and also maximize this torque to improve motor performance. We know that when the rotor and stator fields align perfectly, no torque will be produced. As the angle between them increases, we start generating some torque, and at 90 degrees we get the maximum torque. So, how do we keep these fields at 90 degrees at all times? The first thing we need to know, or measure, is the rotor position. Based on the measured rotor position, we determine the desired orientation of the stator field vector which needs to be orthogonal to the rotor field. The rest of the algorithm is about manipulating the three-phase currents in such a way that they result in this desired stator field vector.
We’ll use this animation to understand how we bring the stator field vector orthogonal to the rotor field. The magenta vector here shows us the vector space representation of the stator magnetic field. The gray vector is our reference that points to the same direction as the rotor magnetic field. We want the magenta vector to lead the reference by 90 degrees. Currently, the magenta vector is 45 degrees ahead of our reference. So, it’s leading by 45 degrees. We see this on the rotating frame on the left. Here’s what the phase-lead looks like on the time-series plot. The phase difference between these periodic waveforms corresponds to 45 degrees. Right now, this magenta stator field vector contributes to torque generation, but since it’s not aligned at 90 degrees with the reference vector or the rotor magnetic field, we’re producing less torque than we actually could. Here’s the trick to align these vectors orthogonally. We split the magenta vector into its components along these two axes. The one along the reference vector or rotor magnetic field is called the direct axis and often represented by the letter d. The other axis that makes 90 degrees with the direct axis is called quadrature axis and represented by the letter q. Here’s how we can break the magenta vector into its direct and quadrature axis components. Once we have these components, the rest of the algorithm is straightforward. We simply force the direct axis component to be zero while allowing the quadrature axis component to grow. Once the direct component diminishes completely, our stator field vector is at exactly 90 degrees with the reference vector. On the right, we see what this looks like in time-domain. Next, we’ll look at this animation to understand how the three-phase currents are changing to keep the stator field orthogonal to the rotor field. We’ll pause here and discuss what the different colored vectors represent. The red, green and blue vectors represent the phase A, B and C currents. The sum of these vectors gives us the stator field vector that is shown in magenta. As in the previous example, the gray vector is our reference which is in the same direction as the rotor field vector. We want the stator field vector to lead the reference by 90 degrees. To make this possible, as we discussed previously, we break the stator field vector into its direct and quadrature axis components and force the direct component to be zero. When we do this, we see how the quadrature component shown in yellow starts to grow. We also observe this on the time-series plot on the right. When it’s in complete quadrature with the reference, we achieve the 90 degrees between stator and rotor fields. On the plot, we see the resulting sinusoidal three-phase currents separated by 120 degrees.
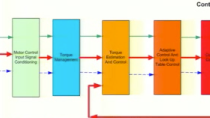
To summarize, we showed how we can break a current vector into its direct and quadrature axis components. Mathematically, this process is called Clarke and Park transforms. The mathematical equations for Clarke and Park transforms are out of scope of this video, but here’s a high-level overview. In field-oriented control, we’re interested in controlling the three-phase currents to be able to control the motor speed and torque. Instead of dealing with the three-phase currents, we convert them into the direct and quadrature currents by Clarke and Park transforms. Why? Because in FOC we’re dealing with AC currents which have sinusoidal waveforms, and we would have hard time controlling these AC signals through PID controllers. When we use Clarke and Park transforms, these translate the stationary stator reference frame into the rotating reference frame. In other words, we don’t need to deal with AC currents anymore but only DC signals, which are the direct and quadrature currents. What we know is that the quadrature current Iq contributes to torque generation, whereas the direct current Id doesn’t produce any torque. So, to get the maximum torque we can use two PI-controllers: one to zero Id and the other one to maximize Iq. Let’s try to show these current control loops on a diagram. We first measure the three-phase currents and then apply the Clarke and Park transforms to convert the three-phase currents to the Iq and Id currents. Next, we compare these measured currents to the desired reference values and feed them to PI controllers, which then output the voltages vq and vd. Note that these voltages are represented in the rotating frame, which need to be converted to three-phase voltages before we send them to the motor. This means we need to do the inverse transforms to find the three-phase voltages.
Let’s summarize what we discussed. With field-oriented control, we can create a stator magnetic field orthogonal to the rotor magnetic fields. This way, we maximize the torque we generate and also reduce the ripples seen in the torque and speed responses of the motor. FOC makes use of Clarke and Park transforms to convert the three-phase AC currents into two DC currents, which are then separately controlled by two PI-control loops.
For more information on the Clarke and Park transforms as well as the FOC algorithm, don’t forget to check out these pages. You can find the links below this video. Next time, we’re going to talk about the space vector pulse width modulation.