Working with Parameter Uncertainty | Robust Control, Part 4
From the series: Robust Control
Brian Douglas
The previous two videos showed a few different ways to quantify how robust a system is to model and plant uncertainty by looking at how much input and output variation it can handle before it no longer meets requirements. In this video, we show another approach. Rather than apply variation to the model as a whole, we apply it to the individual parameters within the model to determine how robust the system is to parameter uncertainty.
Published: 13 Apr 2020
In the last two videos, we showed a few different ways to quantify how robust a system is to model and plant uncertainty by looking at how much input and output variation it can handle before it no longer meets requirements. We looked at how varying the input affected the stability of the system, and we looked at the same by varying the output, and then we looked at varying the input and the output at the same time. In this video, though, rather than apply variation to the model as a whole, we are going to apply it to the individual parameters within the model to determine how robust the system is to parameter uncertainty. I think you’re going to find that this is a really natural way to think about uncertainty in your system, so I hope you stick around for it. I’m Brian, and welcome to a MATLAB Tech Talk.
To demonstrate the power of modeling parameter uncertainty, let’s look at how we might go about controlling a two-cart and spring system. The idea here is that we can adjust the force applied to the handle of the first cart. This is the input into the system. The goal is to move the second cart over to the set point. There are a lot of ways to solve this problem, but I want to show what a solution might look like.
The red line indicated the direction and magnitude of the input force. I don’t know if you caught that, so let’s watch that one more time, and you can see how the force is applied to get the second cart to stop at the set point.
I already said there are a lot of ways to solve this problem; let me show you how I approached it. We can build a linear model of the system dynamics using first principles. We start with the equations of motion, then define the 4 state variables. I’m using cart 1 position and velocity and cart 2 position and velocity. Then we use these state variables to rewrite the equations of motion in state form, and then repackage it into state space matrices. You can pause the video here if you want to study this in more detail, but the main take away is that we have a simple mathematical model of this system in the form of the A, B, C, and D matrices.
Now, we can use this model to develop a feedback control system that will drive the position of the second cart to the set point. I’m going to use full state feedback for the controller, and I’m going to choose the gain using LQR. Let’s go over to MATLAB and see how this is done.
By the way, I’m very loosely following the MathWorks example, Building and Manipulating Uncertain Models, and I’ve left a link to it in the description if you want to try something similar on your own. This first part of this live script is just a graphic reminding you of the problem and showing a cleaner version of the state space model we just derived.
I’m going to arbitrarily set the cart masses and the spring constant to 1, and then build the state space model with the ss command. So, G is the model of the open loop plant. It has one input, force, and it has 4 outputs, each of the four states in our system.
With this model, developing the LQR controller is pretty trivial. I define the Q and R matrices and then solve for the full state feedback gains with the lqr command. If you want to know more about this, check out the MATLAB Tech Talk video on LQR. Link is below.
Ok, now we get the closed loop system model with the feedback command, and our control system design is complete. We can test it and see how it responds to a step command. Here, I’m telling the system to drive both cart positions to the right by one unit, and check this out. After about eight seconds, the positions of both carts have settled at one. You can tell it’s settled since the velocities of both carts go to zero.
So, the controller works! But I want to remind you what we just did. We developed a model of the hardware to calculate what the controller should be. But should we expect this controller to work on the real hardware? Well, if the model perfectly matches the hardware, then yes, for sure it’ll work. But if the model doesn’t perfectly represent the hardware, or if the hardware varies because it changes over time, or there are hardware defects or large manufacturing tolerances, then we don’t know yet if the controller will work with these variations. And like we talked about, this is where the idea of disk margin is helpful. I can check the input/output disk margin for this system and see that at the critical frequency of 1.7 rad/s, the inputs and outputs in the real system can have a gain that varies between 0.76 and 1.3 of what the model claims or phase that varies +/- 15 degrees. If the real variation in the system is between these values, then the controller that we developed with the model will still work.
So, this is how we quantified robustness in the last video, and it is a very useful way to determine margin. But in some cases, it’s not straightforward to relate gain and phase margin back to something physical. Like, it’s hard to quickly see how a variation in spring constant affects the phase or gain of the whole system. For example, what if we buy a batch of springs because we’re building a hundred of these devices and we know every spring will have a slightly different constant. The question is how far out of spec could the spring constant be before we want to reject it prior to installing into the system. It’s not instantly obvious looking at the disk gain and phase margin.
So, in addition to disk margin, let’s approach this problem by asking this question: how much variation in the spring constant and the cart masses can our system handle before instability occurs? A brute force way to answer this is to build hundreds of models, each with a slight variation on m1, m2, and k, and simulate them all and see which systems goes unstable.
This is a Monte Carlo approach to this problem. You specify how the parameters can vary and then run a bunch of simulations to see how it performs.
The problem with a Monte Carlo approach is that you are only testing a finite number of cases within a continuous parameter space. A random distribution of test cases may miss a combination that produces an unstable system. We can improve the odds by increasing the number of cases, or instead, we can check robustness to parameter uncertainty in a more deterministic way using an uncertain parameter model in MATLAB.
The code here is very similar to what we did earlier. We’re going to build the state space equations using the parameters k, m1, and m2 again, except this time, we’re defining them as uncertain real parameters. I’ve arbitrarily said that k can vary 30%, m1 10%, and m2 20%. With the ss command, we can generate an uncertain continuous-time state-space model, which I’ve called G unc.
Using this, we can calculate the uncertain closed system with the feedback command exactly like we did before, so everything is pretty much the same. Except for this! We can check the robust stability margins for the uncertain system with the robstab command.
This command is deterministically solving for the parameter combinations that cause instability and then returning those results. It’s explicitly looking for the worst case. So, it’s similar to a Monte Carlo approach in that we’re looking across the entire parameter space, except that we have guarantees that we’re not missing anything due to random selection.
And it says that our system is robustly stable for the modeled uncertainty, and it turns out we can actually tolerate 2.3 times the parameter uncertainty that we are expecting. So, instead of variations of 30%, 10%, and 20%, we actually will still have a stable system if the spring constant varies by 69%, m1 by 23%, and m2 by 46%. This makes sense because LQR by itself produces a pretty robust control system. This is not the case if it’s paired with a Kalman filter, but that’s a different story. We can look at the smallest parameter combination that destabilizes the system by looking at wcu. If our real hardware has the following spring constant and masses, then we’re in trouble.
Now, here’s something I think is super cool. We can plot things like the step response for an uncertain system model. Here’s the same step response I ran earlier, but now it shows the effects that parameter variation has on it. It does this by plotting 25 random systems within the parameter bounds that we set. And we can see that all 25 of these are stable as expected. So, it’s sort of like the Monte Carlo approach where we verify stability by looking at a finite number of cases.
But check this out. Just to show you that we can miss things with a Monte Carlo approach, let me goback up and change the expected variation to 75, 30, and 50%. We know that some combinations of parameters within this amount of uncertainty will produce an unstable system. And in fact, the robstab command tells us this much. We’re not robustly stable, and we can only tolerate 89% of the modeled uncertainty. So, clearly this isn’t a design we’d be happy with if the parameters truly vary this much.
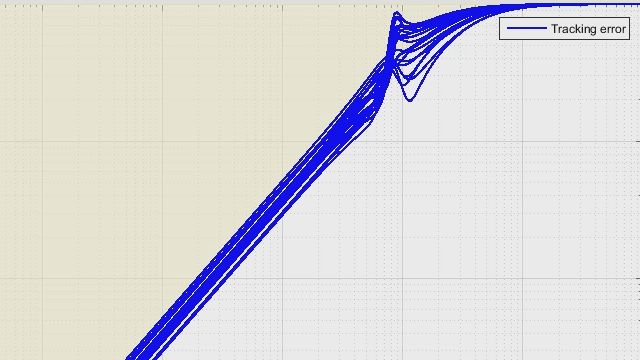
However, if we check the step response where 25 random systems were visualized, we might be tempted to claim that we’re ok since none of these plotted combinations create anything that looks unstable. This is equivalent to running 25 cases in a Monte Carlo approach and then erroneously claiming success.
Let me show you what I mean. I said that wcu is the smallest parameter variation that will destabilize the system. So, let’s assume that we built a system that has this k and m1 value but with an m2 value 5% outside of the minimum acceptable variation. In this case, m2 would be 5% lighter than the lowest stable mass of 0.55 Kg. This combination is still within the parameter uncertainty that we specified above, and if we relied on the 25-case Monte Carlo, then we’d expect this to be ok.
This shouldn’t come as a surprise to you, but it won’t be ok, and we can verify this by plotting its step response. I’m going to extend the simulation time to 100 seconds because it’ll highlight the difference between what the 25 cases are telling us and the reality of the situation.
And there is it. Now, I definitely cherry-picked this case for this video, and in reality we wouldn’t run just 25 Monte Carlo cases. We’d run hundreds or thousands and increase our odds of covering the entire parameter space. But hopefully, with this example you can see how a deterministic approach like we have with an uncertain system model is more reliable for determining robustness to parameter uncertainty than a statistical approach.
All right, that’s where I’m going to leave this video. I hope you can see the value in quantifying parameter uncertainty and using it to assess how robust your system is to parameter variation. And there’s no reason why you have to choose this method over disk margin or classical gain and phase margin. You could look at all of them. Each tells you something different about how your system handles variation, and all of this knowledge will give you a better sense of how robust your system is.
In fact, you can even combine methods. For example, you can add gain and phase uncertainty to the whole system using the umargin command and then check how robust the system is to parameter variations. This method is helpful if you want to see how robust your system is to unmodeled dynamics, like the fact that we didn’t mode the nonlinearities of the spring. I’ve left a link to an example that you can walk through if you’re interested in learning how to quantify the uncertainty that comes from unmodeled dynamics.
Ok, we’ve spent a lot of time in this series talking about determining if our system is robust. In the next video, we’ll look at ways to design your controller from the start with robustness in mind. So, if you don’t want to miss that or any other future Tech Talk videos, don’t forget to subscribe to this channel. And if you want to check out my channel, control system lectures, I cover more control theory topics there as well. Thanks for watching, and I’ll see you next time.