shortestpathtree
Shortest path tree from node
Syntax
Description
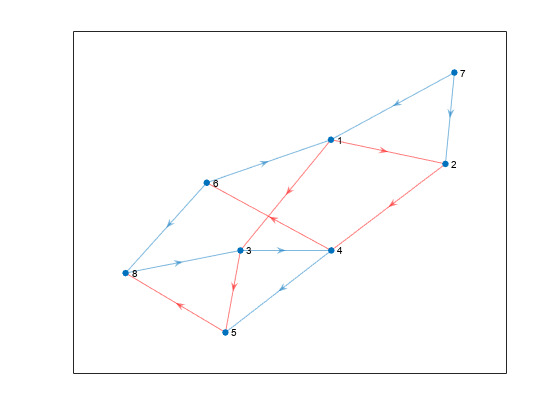
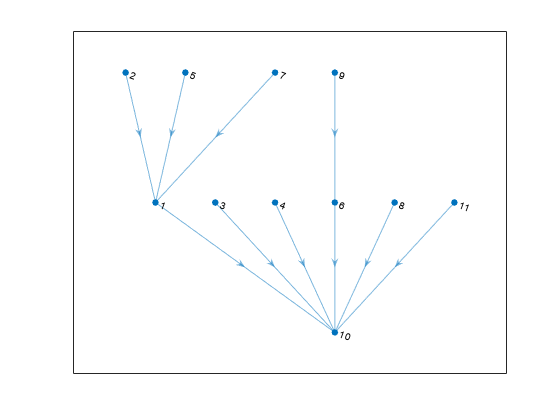
TR = shortestpathtree(G,s)TR, that contains the tree of shortest
paths from source node s to all other nodes in the graph. If the
graph is weighted (that is, G.Edges contains a variable
Weight), then those weights are used as the distances along
the edges in the graph. Otherwise, all edge distances are taken to be
1.
TR = shortestpathtree(___,Name,Value)shortestpathtree(G,s,'OutputForm','vector') returns a numeric
vector that describes the shortest path tree.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
The
shortestpath,shortestpathtree, anddistancesfunctions do not support undirected graphs with negative edge weights, or more generally any graph containing a negative cycle, for these reasons:A negative cycle is a path that leads from a node back to itself, with the sum of the edge weights on the path being negative. If a negative cycle is on a path between two nodes, then no shortest path exists between the nodes, since a shorter path can always be found by traversing the negative cycle.
A single negative edge weight in an undirected graph creates a negative cycle.
Extended Capabilities
Version History
Introduced in R2015b
See Also
shortestpath | distances | nearest | graph | digraph