Faster Finite Fourier Transforms MATLAB
By Cleve Moler and Steve Eddins, MathWorks
We all use FFT s every day without even thinking about it. Cell phones, disk drives, digital cameras, CAT scans and DVDs all involve finite Fourier transforms. One-dimensional transforms with a million points and two-dimensional 1000-by-1000 transforms are common. The key to modern signal and image processing is the ability to do these computations rapidly.
The finite, or discrete, Fourier transform of a complex vector y with n elements yj is another complex vector Y with elements
\[Y_k = \sum_{j=0}^{n-1} \omega^{jk} y_j, \quad k=0, \ldots, n-1\]
The coefficients are paowers of the complex n-th root of unity
\[\omega = e^{\frac{-2\pi i}{n}}\]
Direct application of this definition requires n multiplications and n additions for each of the n components of Y for a total of 2n2 floating point operations. A computer capable of doing one multiplication and one addition every microsecond would require a million seconds, or about 11.5 days, to do a million-point FFT.
Several people discovered fast FFT algorithms independently and many people have since contributed to their development, but it was a 1965 paper by John Tukey of Princeton University and John Cooley of IBM Research that is generally credited as the starting point for the modern usage of the FFT.
Fast finite Fourier transform algorithms have computational complexity O(n log2 n) instead of O(n2). When n is a power of 2, a one-dimensional FFT of length n requires fewer than 5n log2 n floating point operations.
For n = 220, that's a factor of over 20,000 faster than 2n2.
With MATLAB 5.3 and a 266 MHz Pentium laptop, a one-million-point real FFT takes about 6 seconds. With new code in MATLAB 6.0, the same computation takes about 1.2 seconds. This new code is based on FFTW, "The Fastest Fourier Transform in the West," developed by Matteo Frigo and Steven G. Johnson at MIT. Frigo and Johnson won the 1999 J. H. Wilkinson Numerical Software Prize for their work. Their web page has links to their source code and documentation, as well as a wealth of other information about FFTs.
The key to the fast algorithms is the double angle formula for trig functions. Using complex notation, let
\[\omega_n = e^{\frac{-2\pi i}{n}} = \cos(\delta) - i\sin(\delta), \text{where } \delta = \frac{2\pi}{n}\]
We have
\[\omega_{2n^2} = \omega_n\]
Writing this in terms of separate real and imaginary parts produces the double angle formulas,
\[\begin{aligned}\cos(2\delta) &= \cos^2(\delta) - \sin^2(\delta)\\\sin(2\delta) &= 2\cos(\delta)\sin(\delta)\end{aligned}\]
To derive a fast algorithm, start with the basic definition.
\[Y_k = \sum_{j=0}^{n-1} \omega^{jk} y_j, \quad k=0, \ldots, n-1\]
Assume that n is even and that k < n/2. Divide the sum into terms with even and odd subscripts.
\[\begin{aligned}Y_k &= \sum_{\text{even } j} \omega^{jk} y_j + \sum_{\text{odd } j} \omega^{jk} y_j\\ &= \sum_{j=0}^{\frac{n}{2}-1} \omega^{jk} y_{2j} + \omega^k \sum_{j=0}^{\frac{n}{2}-1} \omega^{2jk} y_{2j+1} \end{aligned}\]
The two sums on the right are elements of the FFTs of length n/2 of the portions of y with even and odd subscripts. In order to get the entire FFT of length n, we have to do two FFTs of length n/2, multiply one of these by powers of ω and combine the results.
Now, if n is not only even, but is actually a power of 2, say n = 2m, the process can be repeated. The FFT of length n is expressed in terms of two FFTs of length n/2, then four FFTs of length n/4, and so on until we reach n FFTs of length 1. An FFT of length 1 is just the value itself. The number of steps in the recursion is m. There is O(n) work at each step, so the total amount of work is O(nm) = O(n log2 n).
If n is not a power of 2, it is still possible to express the FFT of length n in terms of several shorter FFTs. If n is not a prime number, an FFT of length n can be expressed in terms of FFTs whose lengths divide n. An FFT of length 100 is two FFTs of length 50, or four FFTs of length 25. An FFT of length 25 can be expressed in terms of FFTs of length 5. Even if n is prime, it is possible to embed the FFT in another whose length can be factored.
The fft function in MATLAB 5 uses fast algorithms only when the length is a product of small primes. The fft function in MATLAB 6 uses fast algorithms for any length, even a prime.
The following demonstration fft function combines two basic ideas. If n is a power of 2, it uses the fast recursive algorithm. If n is not a power of 2, it uses the fast recursion until it reaches an odd length, then sets up the discrete Fourier matrix and uses matrix-vector multiplication. If n = pq where p is a power of 2 and q is odd, the overall computational complexity is O(p log2 p q2).
function y = fftx(x) %FFTX Fast Finite Fourier Transform. x = x(:); n = length(x); omega = exp(-2*pi*i/n); if rem(n,2) == 0
% Recursive divide and conquer. k = (0:n/2-1)'; w = omega.^k; u = fftx(x(1:2:n-1)); v = w.*fftx(x(2:2:n)); y = [u+v; u-v];
else % The Fourier matrix. j = 0:n-1; k = j'; F = omega.^(k*j); y = F*x; end
This program is not a toy. Since it is using the fast recursive algorithm and MATLAB's vector and matrix operations, it offers respectable performance. However MATLAB's new, built-in, FFTW-based code is much faster.
One of the keys to the performance of FFTW involves the same issues we discussed in Cleve's Corner about LAPACK and the BLAS - locality of reference and efficient use of cache. Traditional FFT codes involve complicated indexing schemes called butterflies and bit reversals to access the data. They reference large segments of memory in almost unpredictable patterns. The divide and conquer algorithm moves the data with odd and even subscripts into chunks of contiguous memory, each half the length of the original. The recursion repeats this rearrangement until a point is reached where the current active vector fits in cache. Then a segment of code designed for one specific vector length can do its piece of the computation without touching the main memory.

Frigo and Johnson call these specialized code segments “codelets.” For example, one codelet does a real FFT of length 32. Another codelet does a complex FFT of length 25 and multiplies the result by powers of the 25-th root of unity. FFTW has dozens of these highly specialized, highly optimized codelets. An overall “planner” chooses which codelets to use for each particular vector length. For example, an FFT of length 1000 might be decomposed into 20 FFTs of length 100. Each FFT of length 100 could then be decomposed into four FFTs of length 25.
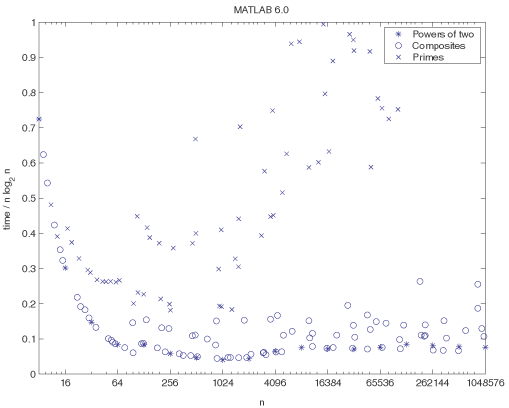
The speed improvements that FFTW provides in MATLAB 6.0 are shown in the graphs. We have measured the execution time required for a real FFT of length n for various values of n on a 400 MHz Pentium machine. The time in microseconds, divided by n log2 n, for MATLAB 5.3 is shown in the first graph, and for MATLAB 6.0 in the second graph. The speedup, which is the ratio of the execution times, is shown in the third graph. The values of n range from 8 to 220, and include powers of 2, composite products of small primes, and primes.

When n is prime, the algorithms in MATLAB 5.3 require time that grows like n2, so the values marked with x’s in the first and third graphs go off scale as n increases.
When n is a power of 2 less than or equal to 216, the times for 5.3 and 6.0 are nearly the same. But the last four *'s show that when n is a power of 2 greater than 65536, the algorithm in 5.3 is about twice as slow as the algorithm in 6.0 because it does not make effective use of cache memory.
When n is not a prime and not a power of 2, the graph of speedup shows that the FFTW algorithms used in MATLAB 6.0 are two to four times faster than our algorithms in MATLAB 5.3.
Published 2001