Benchmarking and Verification
Examples comparing Antenna Toolbox™ simulations with fabricated antennas, measured results, and technical articles.
Featured Examples
Wave Impedance
Uses an elementary dipole and loop antenna to analyze the wave impedance behavior of each radiator in space at a single frequency. The region of space around an antenna has been defined in a variety of ways. The most succinct description is using a 2-or 3-region model. One variation of the 2-region model uses the terms near-field and far-field to identify specific field mechanisms that are dominant. The 3-region model, splits the near-field into a transition zone, wherein a weakly radiative mechanism is at work. Other terms that have been used to describe these zones, include, quasi-static field, reactive field, non-radiative field, Fresnel region, induction zone etc. [1]. Pinning these regions down mathematically presents further challenges as observed with the variety of definitions available across different sources [1]. Understanding the regions around an antenna is critical for both an antenna engineer as well as an electromagnetic compatibility (EMC) engineer. The antenna engineer may want to perform near-field measurements and then compute the far-field pattern. To the EMC engineer, understanding the wave impedance is required for designing a shield with a particular impedance to keep interference out.
Antenna Array Analysis
Create and analyze antenna arrays in Antenna Toolbox™, with emphasis on concepts such as beam scanning, sidelobe level, mutual coupling, element patterns, and grating lobes. The analyses is performed on a 9-element linear array of half-wavelength dipoles.
Plane Wave Excitation - Scattering Solution
Explains how to excite an antenna using a plane wave. The antenna in this case can be thought of as a receiving antenna. A receiving antenna may be viewed as any metal object that scatters an incident electromagnetic field. As a result of scattering an electric current appears on the antenna's surface. The current in turn creates a corresponding electric field. This produces a voltage difference across the feed. This voltage constitutes the received signal. [1]
Read, Visualize and Write MSI Planet Antenna Files
Read an MSI Planet antenna file (.msi or .pln). You can read an MSI file using the msiread function and visualize the data using the polarpattern function. You can also write the data back into the MSI Planet format using the msiwrite function.
Import Measured Field Data and Visualize Radiation Pattern
Visualize a radiation pattern and vector fields from the imported pattern data. Use the patternCustom function to plot the field data in 3D. This function also allows you to view the sliced data. Alternatively, use the polarpattern object to visualize the field data in 2D polar format. The polarpattern function allows you to interact with the data and perform antenna specific measurements. You can also plot the vector fields at a point in space using the fieldsCustom function.
Verification of Far-Field Array Pattern Using Superposition with Embedded Element Patterns
The far-field radiation pattern of a fully excited array can be recreated from the superposition of the individual embedded patterns of each element. The pattern multiplication theorem in array theory states that the far-field radiation pattern of an array is the product of the individual element pattern and the array factor. In the presence of mutual coupling, the individual element patterns are not identical and therefore invalidates the result from pattern multiplication. However, by computing the embedded pattern for each element and using superposition, we can show the equivalence to the array pattern under full excitation.
Analysis of Monopole Impedance
Analyzes the impedance behavior of a monopole at varying mesh resolution/sizes and at a single frequency of operation. The resistance and reactance of the monopole are plotted and compared with the theoretical results. A relative convergence curve is established for the impedance.
Analysis of Dipole Impedance
Analyzes the impedance behavior of a center-fed dipole antenna for various mesh resolution/sizes at a single frequency of operation. The resistance and reactance of the dipole are compared with the theoretical results. A relative convergence curve is established for the impedance.
Monopole Measurement Comparison
Compares the impedance of a monopole analyzed in Antenna Toolbox™ with the measured results. The corresponding antenna was fabricated and measured at the Center for Metamaterials and Integrated Plasmonics (CMIP), Duke University. The monopole is designed for an operating frequency of 2.5 GHz.
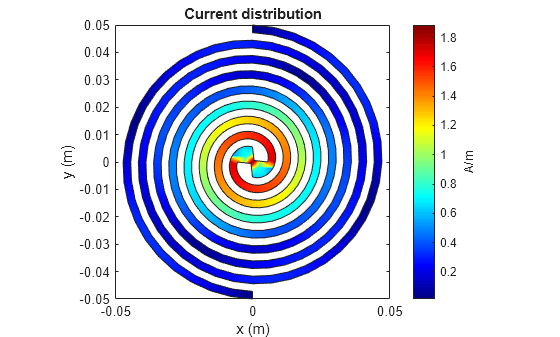
Equiangular Spiral Antenna Design Investigation
Compares results published in [1] for a two-arm equiangular spiral antenna on foamclad backing(ϵr≈ 1), with those obtained using the toolbox model of the spiral antenna of the same dimensions. The spiral antennas belong to the class of frequency-independent antennas. In theory, such antennas may possess an infinite bandwidth when made infinitely large. In reality, a finite feeding region has to be established and the outer extent of the spiral antenna has to be truncated.
Archimedean Spiral Design Investigation
Compares the results published in [1] for an Archimedean spiral antenna with those obtained using the toolbox model of the spiral antenna. The two-arm Archimedean spiral antenna( r = R ϕ ) can be regarded as a dipole, the arms of which have been wrapped into the shape of an Archimedean spiral. This idea came from Edwin Turner around 1954.
Helical Antenna Design
Studies a helical antenna designed in [2] with regard to the achieved directivity. Helical antennas were introduced in 1947 [1]. Since then, they have been widely used in certain applications such as mobile and satellite communications. Helical antennas are commonly used in an axial mode of operation which occurs when the circumference of the helix is comparable to the wavelength of operation. In this mode, the helical antenna has the maximum directivity along its axis and radiates a circularly-polarized wave.
Impedance Matching of Non-resonant (Small) Monopole
Design a double tuning L-section matching network between a resistive source and capacitive load in the form of a small monopole. The L-section consists of two inductors. The network achieves conjugate match and guarantees maximum power transfer at a single frequency.
Comparison of Antenna Array Transmit and Receive Manifold
Calculates and compares the transmit and receive manifolds for a basic half-wavelength dipole antenna array. The array manifold is a fundamental property of antenna arrays, both in transmit and receive configurations. The transmit and receive manifolds are theoretically the same due to the reciprocity theorem. This example validates this equality thus providing an important verification of the calculations performed by the Antenna Toolbox™.
Verification of Far-Field Array Pattern Using Superposition with Embedded Element Patterns
The far-field radiation pattern of a fully excited array can be recreated from the superposition of the individual embedded patterns of each element. The pattern multiplication theorem in array theory states that the far-field radiation pattern of an array is the product of the individual element pattern and the array factor. In the presence of mutual coupling, the individual element patterns are not identical and therefore invalidates the result from pattern multiplication. However, by computing the embedded pattern for each element and using superposition, we can show the equivalence to the array pattern under full excitation.
Design and Analyze Tapered-Slot SIW Filtenna
Create the substrate-integrated-waveguide-based (SIW-based) antipodal filtenna described in [1] with a modified feeding network. A filtenna is a planar antenna with a built-in filter, which can be used to provide frequency agility for communicating at different frequencies without causing any interference to the adjacent bands.You can also use a filtenna to avoid undesired frequencies when you use it as a receiver.
Design a Wideband Antenna for Applications in 8-12 GHz Band
Design a 4-by-4 compact patch antenna array with defected ground structure operating in 8-12 GHz range and compare its simulated analysis results with measured results.
- Since R2025a
- Open Live Script
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)