acousticRoughness
Syntax
Description
roughness = acousticRoughness(audioIn,fs,calibrationFactor)
roughness = acousticRoughness(specificLoudnessIn)
roughness = acousticRoughness(___,Name,Value)roughness = acousticRoughness(audioIn,fs,'SoundField','diffuse')
returns roughness assuming a diffuse sound field.
[
also returns specific roughness strength.roughness,specificRoughness] = acousticRoughness(___)
[
also returns the dominant modulation frequency detected by the algorithm.roughness,specificRoughness,fMod] = acousticRoughness(___)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
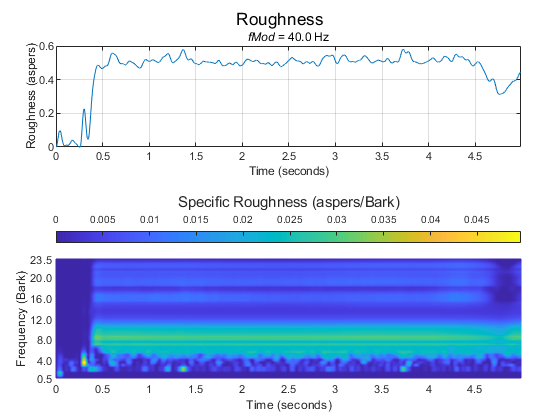
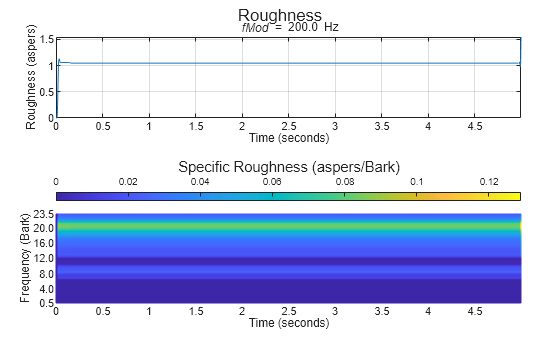
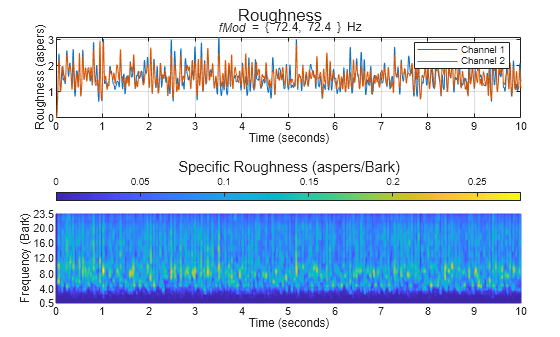
Acoustic roughness strength is a perceptual measurement of modulations in amplitude or
frequency that are too high to discern separately. The acoustic loudness algorithm is
described in [2] and implemented in the
acousticLoudness
function. The acoustic roughness calculation is described in [1]. The algorithm for acoustic
roughness defines the roughness of 1 asper as a 1 kHz tone at 60 dB with a 100% amplitude
modulation at 70 Hz [3]. The algorithm is outlined
as follows:
Where fmod is the detected or
known modulation frequency, cal is a constant ensuring unity roughness of
the reference signal, and ΔL is the perceived modulation depth. If the
modulation frequency is not specified when calling acousticRoughness, it
is auto-detected by peak-picking a frequency-domain representation of the acoustic loudness.
The perceived modulation depth ΔL is calculated by passing rectified
specific loudness bands through ½ octave filters centered around
fmod, followed by a lowpass filter to determine
the envelope.
References
[1] Zwicker, Eberhard, and Hugo Fastl. Psychoacoustics: Facts and Models. Vol. 22. Springer Science & Business Media, 2013.
[2] ISO 532-1:2017(E). "Acoustics – Methods for calculating loudness – Part 1: Zwicker method." International Organization for Standardization.
[3] Kalafata, Stamatina. "Sound Levels, Noise Source Identification and Perceptual Analysis in an Intensive Care Unit." Master's thesis, University of Gothenburg, 2014.
Extended Capabilities
Version History
Introduced in R2021a