comm.MIMOChannel
Filter input signal through MIMO multipath fading channel
Description
The comm.MIMOChannel
System object™ filters an input signal through a multiple-input/multiple-output (MIMO)
multipath fading channel. This object models Rayleigh and Rician fading and represents
the spatial correlation between the links by using the Kronecker model. The channel
filter applies a delay to the input, reflecting the delay of a particular path of the
overall channel. For processing details, see the Algorithms
section.
To filter an input signal through a MIMO multipath fading channel:
Create the
comm.MIMOChannelobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
mimochannel = comm.MIMOChannel
mimochannel = comm.MIMOChannel(Name=Value)comm.MIMOChannel(SampleRate=2) sets the input signal
sample rate to 2.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Input signal sample rate in hertz, specified as a positive scalar.
Data Types: double
Discrete path delay in seconds, specified as a scalar or row vector.
When you set
PathDelaysto a scalar, the MIMO channel is frequency flat.When you set
PathDelaysto a vector, the MIMO channel is frequency selective.
The PathDelays and AveragePathGains properties must be the same length.
Data Types: double
Average path gains in decibels, specified as a scalar or row vector. The
AveragePathGains and PathDelays
properties must be the same length.
Data Types: double
Normalize path gains, specified as one of these logical values:
1(true) — The fading processes are normalized so that the total power of the path gains, averaged over time, is 0 dB.0(false) — The total power of the path gains is not normalized.
The AveragePathGains property specifies the average powers of
the path gains.
Data Types: logical
Fading distribution to use for the channel, specified as
'Rayleigh' or 'Rician'.
Data Types: char | string
K-factor of a Rician fading channel, specified as a positive scalar or a
1-by-NP vector of nonnegative
values. NP is the number of
discrete path delays specified by the PathDelays property.
When you set
KFactorto a scalar, the first discrete path is a Rician fading process with a Rician K-factor ofKFactor. Any remaining discrete paths are independent Rayleigh fading processes.When you set
KFactorto a vector, the discrete path corresponding to a positive element of theKFactorvector is a Rician fading process with a Rician K-factor specified by that element. The discrete path corresponding to any zero-valued elements of theKFactorvector are Rayleigh fading processes. At least one element must be nonzero.
Dependencies
To enable this property, set the FadingDistribution property to
'Rician'.
Data Types: double
Doppler shifts for the line-of-sight components of the multipath Rician
fading channel, specified as a scalar or row vector. Units are in hertz.
This property must be the same size as the KFactor property.
When you set
DirectPathDopplerShiftto a scalar, the value represents the line-of-sight component Doppler shift of the first discrete path. This path exhibits a Rician fading process.When you set
DirectPathDopplerShiftto a row vector, the discrete path corresponding to a positive element of theKFactorvector is a Rician fading process. The corresponding element ofDirectPathDopplerShiftspecifies the line-of-sight component for the Doppler shift of that discrete path.
Dependencies
To enable this property, set the FadingDistribution property to
'Rician'.
Data Types: double
Initial phases for the line-of-sight components of the multipath Rician
fading channel, specified as a scalar or row vector. Units are in radians.
This property must be the same size as the KFactor
property value.
When you set
DirectPathInitialPhaseto a scalar, the value represents the line-of-sight component initial phase of the first discrete path. This path exhibits a Rician fading process.When you set
DirectPathInitialPhaseto a row vector, the discrete path corresponding to a positive element of theKFactorvector is a Rician fading process. The corresponding element ofDirectPathInitialPhasespecifies the line-of-sight component for the initial phase of that discrete path.
Dependencies
To enable this property, set the FadingDistribution property to
'Rician'.
Data Types: double
Maximum Doppler shift for all channel paths, specified as a nonnegative scalar. Units are in hertz.
The maximum Doppler shift limit applies to each channel path. When you set
this property to 0, the channel remains static for the
entire input. You can use the reset
object function to generate a new channel realization. The MaximumDopplerShift property value must be
less than or equal to SampleRate/10/fc
for each path, where fc is the
cutoff frequency factor of the path. For most Doppler spectrum types, the
value of fc is 1. For Gaussian and
bi-Gaussian Doppler spectrum types,
fc is dependent on the Doppler
spectrum structure fields. For more details about how
fc is defined, see the Cutoff
Frequency Factor section.
Data Types: double
Doppler spectrum shape for all channel paths, specified as a Doppler
spectrum structure or a 1-by-NP
cell array of Doppler spectrum structures. These Doppler spectrum structures
must be outputs of the form returned from the doppler function.
NP is the number of discrete
path delays specified by the PathDelays
property. The MaximumDopplerShift property defines the maximum Doppler
shift value that the DopplerSpectrum property permits
when you specify the Doppler spectrum.
When you set
DopplerSpectrumto a single Doppler spectrum structure, all paths have the same specified Doppler spectrum.When you set
DopplerSpectrumto a cell array of Doppler spectrum structures, each path has the Doppler spectrum specified by the corresponding structure in the cell array.
Specify options for the spectrum type by using the
specType input to the doppler function. If you set
the FadingTechnique property to 'Sum of
sinusoids', you must set DopplerSpectrum
to doppler('Jakes').
Dependencies
To enable this property, set the MaximumDopplerShift property to a positive
scalar.
Data Types: struct | cell
Spatial correlation specification, specified as 'Separate Tx
Rx', 'None', or
'Combined'.
Choose
'Separate Tx Rx'to separately specify the transmit and receive spatial correlation matrices from which the number of transmit antennas (NT) and number of receive antennas (NR) are derived.Choose
'None'to specify the number of transmit and receive antennas.Choose
'Combined'to specify a single correlation matrix for the whole channel from which the product of NT and NR is derived.
Data Types: char | string
Number of transmit antennas, specified as a positive integer.
Dependencies
To enable this property, set the SpatialCorrelationSpecification property to
'None' or 'Combined'.
Data Types: double
Number of receive antennas, specified as a positive integer.
Dependencies
To enable this property, set the SpatialCorrelationSpecification property to
'None' or 'Combined'.
Data Types: double
Spatial correlation of the transmitter, specified as an
NT-by-NT
matrix or
NT-by-NT-by-NP
array. NT is the number of
transmit antennas. NP is the
number of discrete path delays specified by the PathDelays
property.
If you set
PathDelaysto a scalar, the channel is frequency flat andTransmitCorrelationMatrixmust be an NT-by-NT Hermitian matrix. The magnitude of any off-diagonal element must be no larger than the geometric mean of the two corresponding diagonal elements.If you set
PathDelaysto a vector, the channel is frequency selective and you can specifyTransmitCorrelationMatrixas one of these options:An NT-by-NT matrix. In this case, each path has the same transmit spatial correlation matrix.
An NT-by-NT-by-NP array. In this case, each path has its own specified transmit spatial correlation matrix.
Dependencies
To enable this property, set the SpatialCorrelationSpecification property to
'Separate Tx Rx'.
Data Types: double
Complex Number Support: Yes
Spatial correlation of the receiver, specified as an
NR-by-NR
matrix or
NR-by-NR-by-NP
array. NR is the number of receive
antennas. NP is the number of
discrete path delays specified by the PathDelays
property.
If you set
PathDelaysto a scalar, the channel is frequency flat, andReceiveCorrelationMatrixmust be an NR-by-NR Hermitian matrix. The magnitude of any off-diagonal element must be no larger than the geometric mean of the two corresponding diagonal elements.If you set
PathDelaysto a vector, the channel is frequency selective and you can specifyReceiveCorrelationMatrixas one of these options:An NR-by-NR matrix. In this case, each path has the same receive spatial correlation matrix.
An NR-by-NR-by-NP array. In this case, each path has its own specified receive spatial correlation matrix.
Dependencies
To enable this property, set the SpatialCorrelationSpecification property to
'Separate Tx Rx'.
Data Types: double
Complex Number Support: Yes
Combined spatial correlation matrix, specified as an
NTR-by-NTR
matrix or
NTR-by-NTR-by-NP
array. NTR =
(NT ✕
NR), and
NP is the number of discrete
delay paths (the length of the PathDelays
property).
If
PathDelaysis a scalar, the channel is frequency flat, andSpatialCorrelationMatrixmust be an NTR-by-NTR Hermitian matrix. The magnitude of any off-diagonal element must be no larger than the geometric mean of the two corresponding diagonal elements.If you set
PathDelaysto a vector, the channel is frequency selective and you can specifySpatialCorrelationMatrixas one of these options:An NTR-by-NTR matrix. In this case, each path has the same combined spatial correlation matrix.
An NTR-by-NTR-by-NP array. In this case, each path has its own specified combined spatial correlation matrix.
Dependencies
To enable this property, set the SpatialCorrelationSpecification property to
'Combined'.
Data Types: double
Complex Number Support: Yes
Antenna selection scheme, specified as 'Off',
'Tx', 'Rx', or 'Tx and
Rx'.
Tx represents transmit antennas, and
Rx represents receive antennas. When you configure
any antenna selection other than the default setting, the object requires
one or more inputs to specify which antennas are selected for signal
transmission. For more information, see Antenna
Selection.
Data Types: char | string
Normalize channel outputs, specified as one of these logical values:
1(true) — The channel outputs are normalized by the number of receive antennas.0(false) — The channel outputs are not normalized.
Data Types: logical
Channel filtering, specified as one of these logical values:
1(true) — The channel accepts an input signal and produces a filtered output signal.0(false) — The object does not accept an input signal, produces no filtered output signal, and outputs only channel path gains. You must specify the duration of the fading process by using theNumSamplesproperty.
Data Types: logical
Output channel path gains, specified as a logical 0
(false) or 1
(true). Set this property to true
to output the channel path gains of the underlying fading process.
Dependencies
To enable this property, set the ChannelFiltering property to
true.
Data Types: logical
Number of samples used for the duration of the fading process, specified as a nonnegative integer.
Tunable: Yes
Dependencies
To enable this property, set the ChannelFiltering property to
false.
Data Types: double
Path gain output data type, specified as 'double' or
'single'.
Dependencies
To enable this property, set the ChannelFiltering property to
false.
Data Types: char | string
Channel model fading technique, specified as 'Filtered Gaussian
noise' or 'Sum of sinusoids'.
Data Types: char | string
Number of sinusoids used to model the fading process, specified as a positive integer.
Dependencies
To enable this property, set the FadingTechnique property to 'Sum of
sinusoids'.
Data Types: double
Source to control the start time of the fading process, specified as
'Property' or 'Input port'.
When you set
InitialTimeSourceto'Property', set the initial time offset by using theInitialTimeproperty.When you set
InitialTimeSourceto'Input port', specify the start time of the fading process by using theinittimeinput argument. The input value can change in consecutive calls to the object.
Dependencies
To enable this property, set the FadingTechnique property to 'Sum of
sinusoids'.
Data Types: char | string
Initial time offset for the fading model in seconds, specified as a nonnegative scalar.
InitialTime must be greater than the end time of the
last frame. When mod(InitialTime/SampleRate) is nonzero, the object rounds the initial time offset up
to the nearest sample position.
Dependencies
To enable this property, set the FadingTechnique property to 'Sum of
sinusoids' and the InitialTimeSource property to
'Property'.
Data Types: double
Source of the random number stream, specified as 'Global
stream' or 'mt19937ar with seed'.
When you specify
'Global stream', the object uses the current global random number stream for random number generation. In this case, theresetobject function resets only the filters.When you specify
'mt19937ar with seed', the object uses the mt19937ar algorithm for random number generation. In this case, theresetobject function resets the filters and reinitializes the random number stream to the value of theSeedproperty.
When input X is a dlarray object, this property
must be set to "GlobalStream".
Data Types: char | string
Initial seed of the mt19937ar random number stream, specified as a
nonnegative integer. When you call the reset object
function, it reinitializes the mt19937ar random number stream to the
Seed value.
Dependencies
To enable this property, set the RandomStream property to 'mt19937ar with
seed'.
Data Types: double
Channel visualization, specified as 'Off',
'Impulse response', 'Frequency
response', 'Impulse and frequency
responses', or 'Doppler spectrum'. When you
set the channel visualization to a value other than
'Off', the selected channel characteristics, such as
impulse response or Doppler spectrum, display in a separate window. For more
information, see Channel Visualization.
Data Types: char | string
Transmit-receive antenna pair to display, specified as a two element row vector. The first element corresponds to the desired transmit antenna, and the second element corresponds to the desired receive antenna. Only a single pair can be displayed.
Dependencies
To enable this property, set the Visualization property to 'Impulse
response', 'Frequency response',
'Doppler spectrum', or 'Impulse and
frequency responses'.
Data Types: double
Path for which the Doppler spectrum is displayed, specified as an integer
in the range [1, NP].
NP is the number of discrete
path delays specified by the PathDelays
property. Use this property to select the discrete path used in constructing
a Doppler spectrum plot.
Dependencies
To enable this property, set the Visualization property to 'Doppler
spectrum'.
Data Types: double
Percentage of samples to display, specified as '25%',
'10%', '50%', or
'100%'. Increasing the percentage improves display
accuracy at the expense of simulation speed.
Dependencies
To enable this property, set the Visualization property to 'Impulse
response', 'Frequency response', or
'Impulse and frequency responses'.
Data Types: char | string
Usage
Syntax
Description
Y = mimochannel(X)X through the MIMO fading
channel and returns the result in Y.
To enable this syntax, set the ChannelFiltering property to true.
Y = mimochannel(X,seltx)seltx.
To enable this syntax set the AntennaSelection property to 'Tx'.
For example, this code shows how to select the first and third transmit antenna index as active.
mimochannel = comm.MIMOChannel('AntennaSelection','Tx');
seltx = [1 0 1];
...
y = mimochannel(x,seltx);Y = mimochannel(X,selrx)selrx.
To enable this syntax set the AntennaSelection property to 'Rx'.
For example, this code shows how to select the second receive antenna index as active.
mimochannel = comm.MIMOChannel('AntennaSelection','Rx');
selrx = [0 1];
...
y = mimochannel(x,selrx);Y = mimochannel(X,seltx,selrx)seltx and
selrx.
To enable this syntax set the AntennaSelection property to 'Tx and
Rx'.
For example, this code shows how to select the first and second transmit antenna and the second receive antenna as active.
mimochannel = comm.MIMOChannel( ...
'AntennaSelection','Tx and Rx');
seltx = [1 1];
selrx = [0 1];
...
y = mimochannel(x,selrx);Y = mimochannel(___,inittime)
To enable this syntax, also set the FadingTechnique property to 'Sum of
sinusoids' and the InitialTimeSource property to 'Input
port'.
pathgains = mimochannel()
To enable this syntax, set the ChannelFiltering property to
false.
pathgains = mimochannel(seltx)seltx.
To enable this syntax set ChannelFiltering property to false and
the AntennaSelection property to 'Tx'.
pathgains = mimochannel(selrx)selrx.
To enable this syntax set the ChannelFiltering property to false and
the AntennaSelection property to 'Rx'.
pathgains = mimochannel(seltx,selrx)seltx and
selrx.
To enable this syntax set the ChannelFiltering property to false and
the AntennaSelection property to 'Tx and
Rx'.
pathgains = mimochannel(___,inittime)
To enable this syntax, also set the FadingTechnique property to 'Sum of
sinusoids' and the InitialTimeSource property to 'Input
port'.
Input Arguments
Input signal, specified as a scalar, an
NS-element column vector,
an
NS-by-NT
or
NS-by-NST
matrix, or a dlarray (Deep Learning Toolbox) object. For more information, see Array Support.
NS is the number of samples.
NT is the number of transmit antennas and is determined by the
TransmitCorrelationMatrixorNumTransmitAntennasproperty values.NST is the number of selected transmit antennas and is determined by the number of elements that are set to
1in the vector provided by theseltxinput.
This object accepts variable-size inputs. After the object is locked, you can change the size of each input channel, but you cannot change the number of channels. For more information, see Variable-Size Signal Support with System Objects.
Data Types: single | double
Complex Number Support: Yes
Select active transmit antennas, specified as a
1-by-NT binary-valued
vector. NT is the number of
transmit antennas. Elements set to 1 identify
selected antenna indices, and the elements set to 0
identify nonselected antenna indices.
Data Types: single | double
Select active receive antennas, specified as a
1-by-NR binary-valued
vector. NR is the number of
receive antennas. Elements set to 1 identify selected
antenna indices, and the elements set to 0 identify
nonselected antenna indices.
Data Types: single | double
Initial time offset for the fading model in seconds, specified as a nonnegative scalar.
When mod(inittime/SampleRate) is nonzero, the initial time offset is rounded up to
the nearest sample position.
Data Types: single | double
Output Arguments
Output signal, returned as an
NS-by-NR
or
NS-by-NSR
matrix, or, if X is a dlarray, as a
dlarray object. For more information, see Array Support.
NS is the number of samples.
NR is the number of receive antennas and is determined by the
ReceiveCorrelationMatrixorNumReceiveAntennasproperty values.NSR is the number of selected receive antennas and is determined by the number of elements that are set to
1in the vector provided by theselrxinput.
Output path gains, returned as an
NS-by-NP-by-NT-by-NR
array with NaN values for the unselected
transmit-receive antenna pairs. pathgains contains
complex values. For more information, see Array Support.
NS is the number of samples.
NP is the number of discrete path delays specified by the
PathDelaysproperty.NT is the number of transmit antennas.
NR is the number of receive antennas.
When you set the ChannelFiltering property to false,
there is no input signal, x and the output is the OutputDataType. When you set the ChannelFiltering property to true,
the output is the same data type as the input signal x.
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Note
Examples
Create a 4-by-2 MIMO channel by using the MIMO channel System object. Modulate and spatially encode data, and then pass the data through the channel.
Generate QPSK-modulated data.
data = randi([0 3],1000,1); modData = pskmod(data,4,pi/4);
Create an orthogonal space-time block encoder System object to encode the modulated data into four spatially separated streams. Then, encode the data.
ostbc = comm.OSTBCEncoder( ... 'NumTransmitAntennas',4, ... 'SymbolRate',1/2); txSig = ostbc(modData);
Create a MIMO channel System object, using name-value pairs to set the properties. The channel consists of two paths, each with a maximum Doppler shift of 5 Hz. Set the SpatialCorrelationSpecification property to 'None', which requires that you specify the number of transmit and receive antennas. Specify four transmit antennas and two receive antennas.
mimochannel = comm.MIMOChannel( ... 'SampleRate',1000, ... 'PathDelays',[0 2e-3], ... 'AveragePathGains',[0 -5], ... 'MaximumDopplerShift',5, ... 'SpatialCorrelationSpecification','None', ... 'NumTransmitAntennas',4, ... 'NumReceiveAntennas',2);
Pass the modulated and encoded signal through the MIMO channel.
rxSig = mimochannel(txSig);
Create a time vector, t, to use for plotting the power of the received signal.
ts = 1/mimochannel.SampleRate; t = (0:ts:(size(txSig,1)-1)*ts)';
Calculate and plot the power of the signal received by antenna 1.
pwrdB = 20*log10(abs(rxSig(:,1))); plot(t,pwrdB) title('Channel Response Power (dBW)') xlabel('Time (s)') ylabel('Power (dBW)')

Generate path gains for a 2-by-2 Rayleigh fading channel and examine the spatial correlation characteristics of the channel realization. Use the release object function to unlock the object to set the AntennaSelection property to 'Tx and Rx' and then confirm the unselected transmit-receive antenna pairs.
Create a 2-by-2 MIMO channel System object with two discrete paths and channel filtering disabled. Each path has different transmit and receive correlation matrices, specified by the TransmitCorrelationMatrix and ReceiveCorrelationMatrix properties.
mimoChan = comm.MIMOChannel( ... 'SampleRate',1000, ... 'PathDelays',[0 1e-3], ... 'AveragePathGains',[3 5], ... 'NormalizePathGains',false, ... 'MaximumDopplerShift',5, ... 'TransmitCorrelationMatrix',cat(3,eye(2),[1 0.1;0.1 1]), ... 'ReceiveCorrelationMatrix',cat(3,[1 0.2;0.2 1],eye(2)), ... 'RandomStream','mt19937ar with seed', ... 'Seed',33, ... 'ChannelFiltering',false);
Generate channel response path gains using the MIMO channel object.
pathGains = mimoChan();
The transmit spatial correlation for the first discrete path at the first receive antenna is specified as an identity matrix in the TransmitCorrelationMatrix property. Confirm that the channel output pathGains exhibits the same statistical characteristics by using the corrcoef function to display the transmit spatial correlation for the first discrete path and the first receive antenna.
corrcoef(squeeze(pathGains(:,1,:,1)))
ans = 2×2 complex
1.0000 + 0.0000i -0.3391 + 0.4285i
-0.3391 - 0.4285i 1.0000 + 0.0000i
The transmit spatial correlation for the second discrete path at the second receive antenna is specified as [1 0.1;0.1 1] in the TransmitCorrelationMatrix property. Confirm that the channel output pathGains exhibits the same statistical characteristics by using the corrcoef function to display the transmit spatial correlation for the second discrete path and the second receive antenna.
corrcoef(squeeze(pathGains(:,2,:,2)))
ans = 2×2 complex
1.0000 + 0.0000i -0.8989 - 0.2663i
-0.8989 + 0.2663i 1.0000 + 0.0000i
The receive spatial correlation for the first discrete path at the second transmit antenna is specified as [1 0.2;0.2 1] in the ReceiveCorrelationMatrix property. Confirm that the channel output pathGains exhibits the same statistical characteristics by using the corrcoef function to display the receive spatial correlation for the first discrete path and the second transmit antenna.
corrcoef(squeeze(pathGains(:,1,2,:)))
ans = 2×2 complex
1.0000 + 0.0000i 0.9170 + 0.3141i
0.9170 - 0.3141i 1.0000 + 0.0000i
The receive spatial correlation for the second discrete path at the first transmit antenna is specified as an identity matrix in the ReceiveCorrelationMatrix property. Confirm that the channel output pathGains exhibits the same statistical characteristics by using the corrcoef function to display the receive spatial correlation for the second discrete path and the first transmit antenna.
corrcoef(squeeze(pathGains(:,2,1,:)))
ans = 2×2 complex
1.0000 + 0.0000i 0.9227 - 0.3435i
0.9227 + 0.3435i 1.0000 + 0.0000i
Create a frequency-selective MIMO channel, and then display its impulse and frequency responses.
Set the sample rate to 10 MHz. Specify path delays and gains using the extended vehicular A (EVA) channel parameters. Set the maximum Doppler shift to 70 Hz.
fs = 10e6; % Hz pathDelays = [0 30 150 310 370 710 1090 1730 2510]*1e-9; % Seconds avgPathGains = [0 -1.5 -1.4 -3.6 -0.6 -9.1 -7 -12 -16.9]; % dB fD = 70; % Hz
Create a 2-by-2 MIMO channel System object, specifying the previously defined parameters and setting channel visualization to plot the impulse and frequency responses. By default, the plot displays the antenna pair corresponding to first transmit and receive antennas.
mimoChan = comm.MIMOChannel(SampleRate=fs, ... PathDelays=pathDelays, ... AveragePathGains=avgPathGains, ... MaximumDopplerShift=fD, ... Visualization='Impulse and frequency responses');
Generate random binary data, and then pass it through the MIMO channel. The impulse response plot enables you to easily identify the individual paths and their corresponding filter coefficients. The frequency response plot shows the frequency-selective nature of the EVA channel.
x = randi([0 1],1000,2); y = mimoChan(x);


To view the antenna pair corresponding to the second transmit and first receive antennas, release the MIMO channel System object, and then set its AntennaPairsToDisplay property to [2 1]. Because the AntennaPairsToDisplay property is nontunable, to change its value, you must release the System object.
release(mimoChan) mimoChan.AntennaPairsToDisplay = [2 1]; y = mimoChan(x);


Create and visualize the Doppler spectra of a MIMO channel that has two paths.
Construct a cell array of Doppler structures to be used in creating the channel. Set the Doppler spectrum of the first path to be bell shaped and the second path to be flat.
dp{1} = doppler('Bell');
dp{2} = doppler('Flat');Create a 2-by-2 MIMO channel System object, specifying two paths and a maximum Doppler shift of 100 Hz, disabling the channel filtering, and enabling the visualization of the Doppler spectrum for the first Doppler path.
mimoChan = comm.MIMOChannel('SampleRate',1000, ... 'PathDelays',[0 0.002], ... 'AveragePathGains',[0 -3], ... 'MaximumDopplerShift',100, ... 'DopplerSpectrum',dp, ... 'ChannelFiltering',false, ... 'NumSamples',10000, ... 'Visualization','Doppler spectrum', ... 'PathsForDopplerDisplay',1);
Use the MIMO channel to generate the Doppler spectrum of the first path. Because the Doppler spectrum plot does not update until its buffer is filled, call the MIMO channel object multiple times to help improve the accuracy of the estimate. Observe that the spectrum has a bell shape and that its minimum and maximum frequencies fall within the limits set by the MaximumDopplerShift property.
for k = 1:25 mimoChan(); end
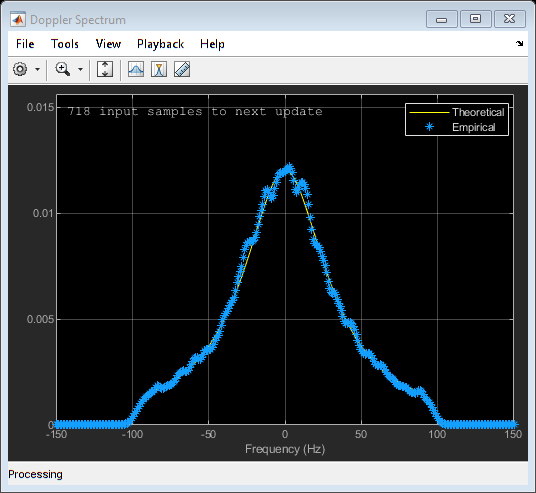
Release the MIMO channel object, and set its PathsForDopplerDisplay property to display the second path. Because the PathsForDopplerDisplay property is nontunable, to change its value, you must release the System object. Call the object multiple times to display the Doppler spectrum of the second path. The results show that the spectrum is flat.
release(mimoChan) mimoChan.PathsForDopplerDisplay = 2; for k = 1:25 y = mimoChan(); end

Show that the channel state is maintained for discontinuous transmissions by using MIMO channel System objects configured to use the sum-of-sinusoids fading technique. Observe discontinuous channel response segments overlaid on a continuous channel response.
Set the channel properties.
fs = 1000; % Sample rate (Hz) pathDelays = [0 2.5e-3]; % Path delays (s) pathPower = [0 -6]; % Path power (dB) fD = 5; % Maximum Doppler shift (Hz) ns = 1000; % Number of samples nsdel = 100; % Number of samples for delayed paths
Define a continuous time span and three discontinuous time segments over which to plot and view the channel response. View a 1000-sample continuous channel response starting at time 0 and three 100-sample channel responses starting at times 0.1, 0.4, and 0.7 seconds, respectively.
to0 = 0.0; to1 = 0.1; to2 = 0.4; to3 = 0.7; t0 = (to0:ns-1)/fs; % Transmission 0 t1 = to1+(0:nsdel-1)/fs; % Transmission 1 t2 = to2+(0:nsdel-1)/fs; % Transmission 2 t3 = to3+(0:nsdel-1)/fs; % Transmission 3
Create a flat-fading 2-by-2 MIMO channel System object, disabling channel filtering and specifying a 1000 Hz sampling rate, the sum-of-sinusoids fading technique, and the number of samples to view. Specify a seed value so that results can be repeated. Use the default InitialTime property setting so that the fading channel is simulated from time 0.
mimoChan1 = comm.MIMOChannel('SampleRate',fs, ... 'MaximumDopplerShift',fD, ... 'RandomStream','mt19937ar with seed', ... 'Seed',17, ... 'FadingTechnique','Sum of sinusoids', ... 'ChannelFiltering',false, ... 'NumSamples',ns);
Create a clone of the MIMO channel System object. Change the number of samples for the delayed paths and the source for the initial time so that you can specify the fading channel offset time as an input argument when calling the System object.
mimoChan2 = clone(mimoChan1);
mimoChan2.InitialTimeSource = 'Input port';
mimoChan2.NumSamples = nsdel;Save the path gain output for the continuous channel response by using the mimoChan1 object and for the discontinuous delayed channel responses by using the mimoChan2 object with initial time offsets provided as input arguments.
pg0 = mimoChan1(); pg1 = mimoChan2(to1); pg2 = mimoChan2(to2); pg3 = mimoChan2(to3);
Compare the number of samples processed by the two channels by using the info method. The results show that mimoChan1 processed 1000 samples and that mimoChan2 processed only 300 samples.
G = info(mimoChan1); H = info(mimoChan2); [G.NumSamplesProcessed H.NumSamplesProcessed]
ans = 1×2
1000 300
Convert the path gains into decibels for the path corresponding to the first transmit and first receive antenna.
pathGain0 = 20*log10(abs(pg0(:,1,1,1))); pathGain1 = 20*log10(abs(pg1(:,1,1,1))); pathGain2 = 20*log10(abs(pg2(:,1,1,1))); pathGain3 = 20*log10(abs(pg3(:,1,1,1)));
Plot the path gains for the continuous and discontinuous cases. The results show that the gains for the three segments match the gain for the continuous case. The alignment of the two shows that the sum-of-sinusoids technique is ideally suited to the simulation of packetized data because the channel characteristics are maintained even when data is not transmitted.
plot(t0,pathGain0,'r--') hold on plot(t1,pathGain1,'b') plot(t2,pathGain2,'b') plot(t3,pathGain3,'b') grid title('Continuous and Discontinuous Channel Response') xlabel('Time (sec)') ylabel('Path Gain (dB)') legend('Continuous','Discontinuous','location','nw')

Demonstrate the advantage of using the sum-of-sinusoids fading technique when simulating a channel with burst data.
Set the simulation parameters such that the sampling rate is 100 kHz, the total simulation time is 100 seconds, and the duty cycle for the burst data is 25%.
fs = 1e5; % Hz tsim = 100; % seconds dutyCycle = 0.25;
Create a flat-fading 2-by-2 MIMO channel System object, specifying the sample rate and using the default filtered Gaussian noise technique.
fgn = comm.MIMOChannel('SampleRate',fs);Create a similar MIMO channel System object, specifying the same sample rate as the previous MIMO channel object but using the sum-of-sinusoids technique. Additionally specify 48 sinusoids and for the fading process start times to be given as an input argument.
sos = comm.MIMOChannel('SampleRate',fs, ... 'FadingTechnique','Sum of sinusoids', ... 'NumSinusoids',48, ... 'InitialTimeSource','Input port');
Run a continuous sequence of random bits through the filtered Gaussian noise MIMO channel object. Use the tic and toc stopwatch timer functions to measure the execution time of the System object call.
tic y = fgn(randi([0 1],fs*tsim,2)); tFGN = toc;
To transmit a data burst each second, pass random bits through the sum-of-sinusoids MIMO channel object by calling it inside of a for loop. Use the tic and toc stopwatch timer functions to measure the execution time.
tic for k = 1:tsim z = sos(randi([0 1],fs*dutyCycle,2),0.5+(k-1)); end tSOS = toc;
Compare the ratio of the sum-of-sinusoids execution time to the filtered Gaussian noise execution time. The ratio is less than one, which indicates that the sum-of-sinusoids technique is faster than the filtered Gaussian noise technique.
tSOS/tFGN
ans = 0.1948
Using one MIMO channel System object™ and two identically configured channel filter System objects, switch a link-level simulation between 3-by-2 downlink and reciprocal 2-by-3 uplink signal transmissions.
Define system parameters.
modOrder = 256; % Modulation order Nant1 = 3; % Number of 'transmit' antennas Nant2 = 2; % Number of 'receive' antennas Rs = 1e6; % Sample rate pd = [0 1.5 2.3]*1e-6; % Path delays frmLen = 1e3; % Frame length
Create a MIMO channel System object™, configuring it for path gain generation by disabling channel filtering.
chan = comm.MIMOChannel( ... 'SampleRate',Rs, ... 'PathDelays',pd, ... 'AveragePathGains',[1.5 1.2 0.2], ... 'MaximumDopplerShift',300, ... 'SpatialCorrelationSpecification','none', ... 'NumTransmitAntennas',Nant1, ... 'NumReceiveAntennas',Nant2, ... 'ChannelFiltering',false, ... 'NumSamples',frmLen);
Create identical channel filter System objects for both transmission directions: one channel filter for the Nant1-by-Nant2 downlink channel (3 transmit antennas to 2 receive antennas) and a reciprocal channel filter for the Nant2-by-Nant1 uplink channel (2 transmit antennas to 3 receive antennas).
chanFiltDownlink = comm.ChannelFilter( ... 'SampleRate',Rs, ... 'PathDelays',pd); chanFiltUplink = clone(chanFiltDownlink);
Downlink Transmission
Generate random path gains for one frame of the downlink 3-by-2 channel. Pass randomly generated 256-QAM signals through the 3-by-2 downlink channel.
pgDownlink = chan(); x = qammod(randi([0 modOrder-1],frmLen,Nant1),modOrder); yDL = chanFiltDownlink(x,pgDownlink);
Uplink Transmission
Switch the link direction. Run the channel object to generate another frame of path gains, permuting its 3rd (Tx) and 4th (Rx) dimensions for the reciprocal uplink 2-by-3 channel. Pass randomly generated 256-QAM signals through the 2-by-3 reciprocal uplink channel.
pgUplink = permute(chan(),[1 2 4 3]); x = qammod(randi([0 modOrder-1],frmLen,Nant2),modOrder); yUL = chanFiltUplink(x,pgUplink);
Downlink and Uplink Array Dimensions
Show the sizes of the downlink and uplink path gain arrays returned by the MIMI channel object as an -by--by--by- array.
is the number of samples.
is the number of path delays.
is the number of transmit antennas.
Nant1for downlink andNant2for uplink.is the number of receive antennas.
Nant2for downlink andNant1for uplink.
size(pgDownlink)
ans = 1×4
1000 3 3 2
size(pgUplink)
ans = 1×4
1000 3 2 3
Show the size of the channel output matrices returned by the MIMI channel object as an -by- matrix. is the number of samples. is the number of receive antennas.
size(yDL)
ans = 1×2
1000 2
size(yUL)
ans = 1×2
1000 3
More About
The comm.MIMOChannel object supports an input signal
represented in an array, dlarray (Deep Learning Toolbox), or gpuArray (Parallel Computing Toolbox).
If
Xis specified as agpuArray,Yis returned as agpuArrayobject.If
Xis specified as adlarray,Yis returned as adlarrayobject.If
Xis adlarrayholding agpuArray, then thepathgainsare generated on the GPU, otherwise thepathgainsare generated on the CPU.The number of batch observations (NB) is an optional dimension that can be added to the input for all supported data types. Variable NB is not supported. When the NB dimension is included:
Where:
NS is the number of samples.
NT is the number of transmit antennas and is determined by the
TransmitCorrelationMatrixorNumTransmitAntennasproperty values.NP is the number of discrete path delays specified by the
PathDelaysproperty.NR is the number of receive antennas and is determined by the
ReceiveCorrelationMatrixorNumReceiveAntennasproperty values.
Note
When using batch processing:
The
Visualizationproperty setting must be'Off".The
AntennaSelectionproperty setting must be'Off'.The
RandomStreamproperty setting must be'Global stream'.
For a list of Communications Toolbox™ features that support dlarray objects, see AI for Wireless.
Algorithms
The fading processing per link is described in Methodology for Simulating Multipath Fading Channels and assumes the same parameters for all (NT × NR) links of the MIMO channel. Each link comprises all multipaths for that link.
The Kronecker model assumes that the spatial correlations at the transmit and receive sides are separable. Equivalently, the direction of departure (DoD) and directions of arrival (DoA) spectra are assumed to be separable. The full correlation matrix is:
The ⊗ symbol represents the Kronecker product.
Rt is the correlation matrix at the transmit side, , and is of size NT-by-NT.
Rr is the correlation matrix at the receive side, , and is of size NR-by-NR.
You can obtain a realization of the MIMO channel matrix as:
A is an NR-by-NT matrix of independent identically distributed complex Gaussian variables with zero mean and unit variance.
The cutoff frequency factor, fc, is dependent on the type of Doppler spectrum.
For any Doppler spectrum type other than Gaussian and bi-Gaussian, fc equals 1.
For a
doppler('Gaussian')spectrum type, fc equalsNormalizedStandardDeviation.For a
doppler('BiGaussian')spectrum type:If the
PowerGains(1)andNormalizedCenterFrequencies(2)field values are both0, then fc equalsNormalizedStandardDeviation(1).If the
PowerGains(2)andNormalizedCenterFrequencies(1)field values are both0, then fc equalsNormalizedStandardDeviation(2).If the
NormalizedCenterFrequenciesfield value is[0,0]and theNormalizedStandardDeviationfield has two identical elements, then fc equalsNormalizedStandardDeviation(1).In all other cases, fc equals 1.
When the object is in antenna-selection mode, it uses these algorithms to process an input signal.
All random path gains are always generated and keep evolving for each link, whether or not a given link is selected. The path gain values output for the nonselected links are populated with
NaN.The spatial correlation applies to only the selected transmit and receive antennas, and the correlation coefficients are the corresponding entries in the transmit, receive, or combined correlation matrices. That is, the spatial correlation matrix for the selected transmit or receive antennas is a submatrix of the transmit, receive, or combined spatial correlation matrix property value.
For signal paths that are associated with nonactive antennas, a signal with zero power is transmitted to the channel filter.
Channel output normalization happens over the number of selected receive antennas.
References
[1] Oestges, Claude, and Bruno Clerckx., MIMO Wireless Communications: From Real-World Propagation to Space-Time Code Design. 1st ed. Boston, MA: Elsevier, 2007.
[2] Correia, Luis M., and European Cooperation in the Field of Scientific and Technical Research (Organization), eds. Mobile Broadband Multimedia Networks: Techniques, Models and Tools for 4G. 1st ed. Amsterdam; Boston: Elsevier/Academic Press, 2006.
[3] Kermoal, J.P., L. Schumacher, K.I. Pedersen, P.E. Mogensen, and F. Frederiksen. “A Stochastic MIMO Radio Channel Model with Experimental Validation.” IEEE® Journal on Selected Areas in Communications 20, no. 6 (August 2002): 1211–26. https://doi.org/10.1109/JSAC.2002.801223.
[4] Jeruchim, Michel C., Philip Balaban, and K. Sam Shanmugan. Simulation of Communication Systems. Second edition. Boston, MA: Springer US, 2000.
[5] Patzold, M., Cheng-Xiang Wang, and B. Hogstad. “Two New Sum-of-Sinusoids-Based Methods for the Efficient Generation of Multiple Uncorrelated Rayleigh Fading Waveforms.” IEEE Transactions on Wireless Communications 8, no. 6 (June 2009): 3122–31. https://doi.org/10.1109/TWC.2009.080769.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
This System object supports GPU array inputs. For more information, see Accelerate Simulation Using GPUs.
Usage notes and limitations:
To enable GPU processing, input signal (
X) must be agpuArrayobject.Setting
ChannelFilteringtofalseand all the corresponding syntaxes are not supportedSetting
AntennaSelectionto'Tx','Rx', or'Tx and Rx'and all the corresponding syntaxes are not supported.Setting
RandomStreamto'mt19937ar with seed'and all the corresponding properties are not supported.
Version History
Introduced in R2012aThe comm.MIMOChannel object adds support for dlarray (Deep Learning Toolbox)
object processing for deep learning applications. When input X is a
dlarray object, the RandomStream property
must be set to "GlobalStream".
The comm.MIMOChannel
System object adds support for gpuArray (Parallel Computing Toolbox) object processing to run
code on a graphics processing unit (GPU). For more information, see Extended Capabilities.
The channel visualization feature now presents:
Configuration settings in the bottom toolbar on the plot window.
Plots side-by-side in one window when you select the
Impulse and frequency responsechannel visualization option.
See Also
Objects
comm.AWGNChannel|comm.RayleighChannel|comm.RicianChannel|comm.RayTracingChannel|comm.ChannelFilter
Blocks
Topics
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)