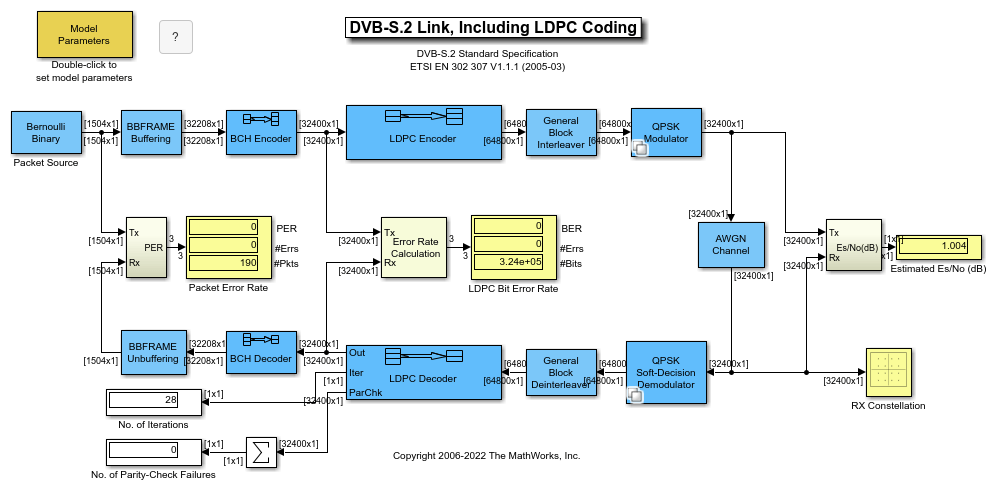
LDPC Decoder
Decode binary low-density parity-check (LDPC) code
Libraries:
Communications Toolbox /
Error Detection and Correction /
Block
Description
The LDPC Decoder block uses the belief propagation algorithm to decode a binary LDPC code, which is input to the block as the soft-decision output (log-likelihood ratio of received bits) from demodulation. The block decodes generic binary LDPC codes where no patterns in the parity-check matrix are assumed. For more information, see Belief Propagation Decoding.
The input and output are discrete-time signals. The ratio of the output sample time to the input sample time is:
N/K when only the information-part of the codeword is decoded
1 when the entire codeword is decoded
N is the length of the received signal and must be in the range (0, 231). K is the length of the uncoded message and must be less than N.
This icon shows all ports, including optional ports, for the LDPC Decoder block.
![]()
Examples
Extended Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
References
[1] Gallager, Robert G. Low-Density Parity-Check Codes. Cambridge, MA: MIT Press, 1963.