Parallel Interconnection of Passive Systems
This example illustrates the properties of a parallel interconnection of passive systems.
Parallel Interconnection of Passive Systems
Consider an interconnection of two subsystems and in parallel. The interconnected system maps the input to the output .
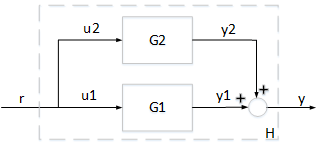
If both systems and are passive, then the interconnected system is guaranteed to be passive. Take for example
.
Both systems are passive.
G1 = tf([0.1,1],[1,2]); isPassive(G1)
ans = logical
1
G2 = tf([1,2,1],[1,3,10]); isPassive(G2)
ans = logical
1
We can therefore expect their parallel interconnection to be passive, as confirmed by
H = parallel(G1,G2); isPassive(H)
ans = logical
1
Passivity Indices for Parallel Interconnection
There is a relationship between the passivity indices of and and the passivity indices of the interconnected system . Let and denote the input passivity indices for and , and let and denote the output passivity indices. If all these indices are nonnegative, then the input passivity index and the output passivity index for the parallel interconnection satisfy
In other words, we can infer some minimum level of input and output passivity for the parallel connection from the input and output passivity indices of and . For details, see the paper by Yu, H., "Passivity and dissipativity as design and analysis tools for networked control systems," Chapter 2, PhD Thesis, University of Notre Dame, 2012. Verify the lower bound for the input passivity index .
% Input passivity index for G1 nu1 = getPassiveIndex(G1,'input'); % Input passivity index for G2 nu2 = getPassiveIndex(G2,'input'); % Input passivity index for H nu = getPassiveIndex(H,'input')
nu = 0.3777
% Lower bound
nu1+nu2ans = 0.1474
Similarly, verify the lower bound for the output passivity index of .
% Output passivity index for G1 rho1 = getPassiveIndex(G1,'output'); % Output passivity index for G2 rho2 = getPassiveIndex(G2,'output'); % Output passivity index for H rho = getPassiveIndex(H,'output')
rho = 0.6443
% Lower bound
rho1*rho2/(rho1+rho2)ans = 0.2098