Cluster with a Competitive Neural Network
The neurons in a competitive layer distribute themselves to recognize frequently presented input vectors.
Architecture
The architecture for a competitive network is shown below.
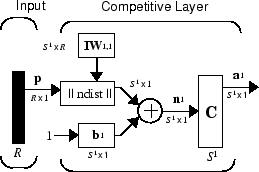
The ‖ dist ‖ box in this figure accepts the input vector
p and the input weight matrix IW1,1, and produces a vector
having S1 elements. The elements are the negative of the
distances between the input vector and vectors
iIW1,1 formed from the rows of the input
weight matrix.
Compute the net input n1 of a competitive layer by finding the negative distance between input vector p and the weight vectors and adding the biases b. If all biases are zero, the maximum net input a neuron can have is 0. This occurs when the input vector p equals that neuron's weight vector.
The competitive transfer function accepts a net input vector for a layer and returns neuron outputs of 0 for all neurons except for the winner, the neuron associated with the most positive element of net input n1. The winner's output is 1. If all biases are 0, then the neuron whose weight vector is closest to the input vector has the least negative net input and, therefore, wins the competition to output a 1.
Reasons for using biases with competitive layers are introduced in Bias Learning Rule (learncon).
Create a Competitive Neural Network
You can create a competitive neural network with the function competlayer. A simple example shows
how this works.
Suppose you want to divide the following four two-element vectors into two classes.
p = [.1 .8 .1 .9; .2 .9 .1 .8]
p =
0.1000 0.8000 0.1000 0.9000
0.2000 0.9000 0.1000 0.8000
There are two vectors near the origin and two vectors near (1,1).
First, create a two-neuron competitive layer.:
net = competlayer(2);
Now you have a network, but you need to train it to do the classification job.
The first time the network is trained, its weights will initialized to the centers
of the input ranges with the function midpoint. You can check see these
initial values using the number of neurons and the input data:
wts = midpoint(2,p)
wts =
0.5000 0.5000
0.5000 0.5000
These weights are indeed the values at the midpoint of the range (0 to 1) of the inputs.
The initial biases are computed by initcon, which gives
biases = initcon(2)
biases =
5.4366
5.4366
Recall that each neuron competes to respond to an input vector p. If the biases are all 0, the neuron whose weight vector is closest to p gets the highest net input and, therefore, wins the competition, and outputs 1. All other neurons output 0. You want to adjust the winning neuron so as to move it closer to the input. A learning rule to do this is discussed in the next section.
Kohonen Learning Rule (learnk)
The weights of the winning neuron (a row of the input weight matrix) are adjusted with the Kohonen learning rule. Supposing that the ith neuron wins, the elements of the ith row of the input weight matrix are adjusted as shown below.
The Kohonen rule allows the weights of a neuron to learn an input vector, and because of this it is useful in recognition applications.
Thus, the neuron whose weight vector was closest to the input vector is updated to be even closer. The result is that the winning neuron is more likely to win the competition the next time a similar vector is presented, and less likely to win when a very different input vector is presented. As more and more inputs are presented, each neuron in the layer closest to a group of input vectors soon adjusts its weight vector toward those input vectors. Eventually, if there are enough neurons, every cluster of similar input vectors will have a neuron that outputs 1 when a vector in the cluster is presented, while outputting a 0 at all other times. Thus, the competitive network learns to categorize the input vectors it sees.
The function learnk is used to perform the Kohonen
learning rule in this toolbox.
Bias Learning Rule (learncon)
One of the limitations of competitive networks is that some neurons might not always be allocated. In other words, some neuron weight vectors might start out far from any input vectors and never win the competition, no matter how long the training is continued. The result is that their weights do not get to learn and they never win. These unfortunate neurons, referred to as dead neurons, never perform a useful function.
To stop this, use biases to give neurons that only win the competition rarely (if ever) an advantage over neurons that win often. A positive bias, added to the negative distance, makes a distant neuron more likely to win.
To do this job a running average of neuron outputs is kept. It is equivalent to
the percentages of times each output is 1. This average is used to update the biases
with the learning function learncon so that the biases of frequently active neurons become
smaller, and biases of infrequently active neurons become larger.
As the biases of infrequently active neurons increase, the input space to which those neurons respond increases. As that input space increases, the infrequently active neuron responds and moves toward more input vectors. Eventually, the neuron responds to the same number of vectors as other neurons.
This has two good effects. First, if a neuron never wins a competition because its weights are far from any of the input vectors, its bias eventually becomes large enough so that it can win. When this happens, it moves toward some group of input vectors. Once the neuron's weights have moved into a group of input vectors and the neuron is winning consistently, its bias will decrease to 0. Thus, the problem of dead neurons is resolved.
The second advantage of biases is that they force each neuron to classify roughly the same percentage of input vectors. Thus, if a region of the input space is associated with a larger number of input vectors than another region, the more densely filled region will attract more neurons and be classified into smaller subsections.
The learning rates for learncon are typically set an order
of magnitude or more smaller than for learnk to make sure that the running average is accurate.
Training
Now train the network for 500 epochs. You can use either train or adapt.
net.trainParam.epochs = 500; net = train(net,p);
Note that train for competitive networks uses
the training function trainru. You can verify this by
executing the following code after creating the network.
net.trainFcn
ans = trainru
For each epoch, all training vectors (or sequences) are each presented once in a different random order with the network and weight and bias values updated after each individual presentation.
Next, supply the original vectors as input to the network, simulate the network, and finally convert its output vectors to class indices.
a = sim(net,p); ac = vec2ind(a)
ac =
1 2 1 2
You see that the network is trained to classify the input vectors into two groups, those near the origin, class 1, and those near (1,1), class 2.
It might be interesting to look at the final weights and biases.
net.IW{1,1}ans =
0.1000 0.1500
0.8500 0.8500net.b{1}ans =
5.4367
5.4365 (You might get different answers when you run this problem, because a random seed is used to pick the order of the vectors presented to the network for training.) Note that the first vector (formed from the first row of the weight matrix) is near the input vectors close to the origin, while the vector formed from the second row of the weight matrix is close to the input vectors near (1,1). Thus, the network has been trained—just by exposing it to the inputs—to classify them.
During training each neuron in the layer closest to a group of input vectors adjusts its weight vector toward those input vectors. Eventually, if there are enough neurons, every cluster of similar input vectors has a neuron that outputs 1 when a vector in the cluster is presented, while outputting a 0 at all other times. Thus, the competitive network learns to categorize the input.
Graphical Example
Competitive layers can be understood better when their weight vectors
and input vectors are shown graphically. The diagram below shows 48 two-element
input vectors represented with + markers.
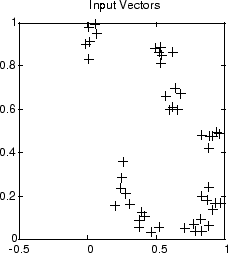
The input vectors above appear to fall into clusters. You can use a competitive network of eight neurons to classify the vectors into such clusters.
Try Competitive Learning to see a dynamic example of competitive learning.