Learn Pre-Emphasis Filter Using Deep Learning
This example shows how to use a convolutional deep network to learn a pre-emphasis filter for speech recognition. The example uses a learnable short-time Fourier transform (STFT) layer to obtain a time-frequency representation suitable for use with 2-D convolutional layers. The use of a learnable STFT enables a gradient-based optimization of the pre-emphasis filter weights.
Data
Clone or download the Free Spoken Digit Dataset (FSDD), available at https://github.com/Jakobovski/free-spoken-digit-dataset. FSDD is an open data set, which means that it can grow over time. This example uses the version committed on 08/20/2020 which consists of 3000 recordings of the English digits 0 through 9 obtained from six speakers. The data is sampled at 8000 Hz.
This example assumes that you have downloaded the data into the folder corresponding to the value of tempdir in MATLAB. If you use a different folder, substitute that folder name for tempdir in the following code. Use audioDatastore to manage data access and ensure random division of data into training and test sets.
pathToRecordingsFolder = fullfile(tempdir,'free-spoken-digit-dataset','recordings'); ads = audioDatastore(pathToRecordingsFolder);
Use the filenames2labels function to obtain a categorical vector of labels from the FSDD files. Display the count of each label in the data set.
lbls = filenames2labels(ads,ExtractBefore="_");
ads.Labels = lbls;
countlabels(lbls)ans=10×3 table
Label Count Percent
_____ _____ _______
0 300 10
1 300 10
2 300 10
3 300 10
4 300 10
5 300 10
6 300 10
7 300 10
8 300 10
9 300 10
Split the FSDD into training and test sets maintaining equal class proportions in each subset. For reproducible results, set the random number generator to its default value. Eighty percent, or 2400 recordings, are used for training. The remaining 600 recordings, 20% of the total, are held out for testing. Shuffle the files in the datastore once before creating the training and test sets.
rng default;
ads = shuffle(ads);
[adsTrain,adsTest] = splitEachLabel(ads,0.8,0.2);The recordings in FSDD are not equal in length. Use a transform so that each read from the datastore is padded or truncated to 8192 samples. The data are additionally cast to single-precision and a z-score normalization is applied.
transTrain = transform(adsTrain,@(x,info)helperReadData(x,info),'IncludeInfo',true); transTest = transform(adsTest,@(x,info)helperReadData(x,info),'IncludeInfo',true);
Deep Convolutional Neural Network (DCNN) Architecture
This example uses a custom training loop with the following deep convolutional network.
numF = 12;
dropoutProb = 0.2;
layers = [
sequenceInputLayer(1,'Name','input','MinLength',8192,...
'Normalization',"none")
convolution1dLayer(5,1,"name","pre-emphasis-filter",...
"WeightsInitializer",@(sz)kronDelta(sz),"BiasLearnRateFactor",0)
stftLayer('Window',hamming(1280),'OverlapLength',900,...
'Name','STFT')
convolution2dLayer(5,numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,2*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,2*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
dropoutLayer(dropoutProb)
globalAveragePooling2dLayer
fullyConnectedLayer(numel(categories(ads.Labels)))
softmaxLayer
];
dlnet = dlnetwork(layers);The sequence input layer is followed by a 1-D convolution layer consisting of a single filter with 5 coefficients. This is a finite impulse response filter. Convolutional layers in deep learning networks by default implement an affine operation on the input features. To obtain a strictly linear (filtering) operation, use the default 'BiasInitializer' which is 'zeros' and set the bias learn rate factor of the layer to 0. This means that the bias is initialized to 0 and never changes during training. The network uses a custom initialization of the filter weights to be a scaled Kronecker delta sequence. This is an allpass filter, which performs no filtering of the input. The code for the allpass filter weight initializer is shown here.
function delta = kronDelta(sz) % This function is only for use in the "Learn Pre-Emphasis Filter using % Deep Learning" example. It may change or be removed in a % future release. L = sz(1); delta = zeros(L,sz(2),sz(3),'single'); delta(1) = 1/sqrt(L); end
stftLayer takes the filtered batch of input signals and obtains their magnitude STFTs. The magnitude STFT is a 2-D representation of the signal, which is amenable to use in 2-D convolutional networks.
While the weights of the STFT are not changed here during training, the layer supports backpropagation, which enables the filter coefficients in the "pre-emphasis-filter" layer to be learned.
Network Training
Set the training options for the custom training loop. Use 70 epochs with a minibatch size of 128. Set the initial learn rate to 0.001.
NumEpochs = 70; miniBatchSize = 128; learnRate = 0.001;
In the custom training loop, use a minibatchqueue object. The processSpeechMB function reads in a minibatch and applies a one-hot encoding scheme to the labels.
mbqTrain = minibatchqueue(transTrain,2,... 'MiniBatchSize',miniBatchSize,... 'MiniBatchFormat', {'CBT','CB'}, ... 'MiniBatchFcn', @processSpeechMB);
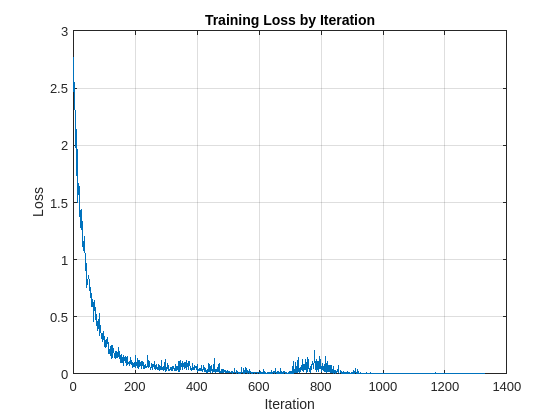
Train the network and plot the loss for each iteration. Use an Adam optimizer to update the network learnable parameters. To plot the loss as training progress, set the value of progress in the following code to "training-progress".
progress = "final-loss"; if progress == "training-progress" figure lineLossTrain = animatedline; ylim([0 inf]) xlabel("Iteration") ylabel("Loss") grid on end % Initialize some training loop variables trailingAvg = []; trailingAvgSq = []; iteration = 0; lossByIteration = 0; % Loop over epochs and time the epochs start = tic; for epoch = 1:NumEpochs reset(mbqTrain) shuffle(mbqTrain) % Loop over mini-batches while hasdata(mbqTrain) iteration = iteration + 1; % Get the next minibatch and one-hot coded targets [dlX,Y] = next(mbqTrain); % Evaluate the model gradients and loss [gradients, loss, state] = dlfeval(@modelGradSTFT,dlnet,dlX,Y); if progress == "final-loss" lossByIteration(iteration) = loss; end % Update the network state dlnet.State = state; % Update the network parameters using an Adam optimizer [dlnet,trailingAvg,trailingAvgSq] = adamupdate(... dlnet,gradients,trailingAvg,trailingAvgSq,iteration,learnRate); % Display the training progress D = duration(0,0,toc(start),'Format','hh:mm:ss'); if progress == "training-progress" addpoints(lineLossTrain,iteration,loss) title("Epoch: " + epoch + ", Elapsed: " + string(D)) end end disp("Training loss after epoch " + epoch + ": " + loss); end
Training loss after epoch 1: 1.5686 Training loss after epoch 2: 1.2063 Training loss after epoch 3: 0.70384 Training loss after epoch 4: 0.50291 Training loss after epoch 5: 0.35332 Training loss after epoch 6: 0.22536 Training loss after epoch 7: 0.14302 Training loss after epoch 8: 0.14749 Training loss after epoch 9: 0.1436 Training loss after epoch 10: 0.092127 Training loss after epoch 11: 0.053437 Training loss after epoch 12: 0.059123 Training loss after epoch 13: 0.07433 Training loss after epoch 14: 0.066282 Training loss after epoch 15: 0.11964 Training loss after epoch 16: 0.087663 Training loss after epoch 17: 0.069451 Training loss after epoch 18: 0.11175 Training loss after epoch 19: 0.044604 Training loss after epoch 20: 0.064503 Training loss after epoch 21: 0.050275 Training loss after epoch 22: 0.022125 Training loss after epoch 23: 0.092534 Training loss after epoch 24: 0.1393 Training loss after epoch 25: 0.015846 Training loss after epoch 26: 0.022516 Training loss after epoch 27: 0.01798 Training loss after epoch 28: 0.012391 Training loss after epoch 29: 0.0068496 Training loss after epoch 30: 0.036968 Training loss after epoch 31: 0.014514 Training loss after epoch 32: 0.0055389 Training loss after epoch 33: 0.0080868 Training loss after epoch 34: 0.0097247 Training loss after epoch 35: 0.0067841 Training loss after epoch 36: 0.0073048 Training loss after epoch 37: 0.0068763 Training loss after epoch 38: 0.064052 Training loss after epoch 39: 0.029343 Training loss after epoch 40: 0.055245 Training loss after epoch 41: 0.20821 Training loss after epoch 42: 0.052951 Training loss after epoch 43: 0.034677 Training loss after epoch 44: 0.020905 Training loss after epoch 45: 0.077562 Training loss after epoch 46: 0.0055673 Training loss after epoch 47: 0.015712 Training loss after epoch 48: 0.011886 Training loss after epoch 49: 0.0063345 Training loss after epoch 50: 0.0030241 Training loss after epoch 51: 0.0033596 Training loss after epoch 52: 0.0042235 Training loss after epoch 53: 0.0054001 Training loss after epoch 54: 0.0037229 Training loss after epoch 55: 0.0042717 Training loss after epoch 56: 0.0030938 Training loss after epoch 57: 0.0024514 Training loss after epoch 58: 0.005746 Training loss after epoch 59: 0.0027509 Training loss after epoch 60: 0.0069394 Training loss after epoch 61: 0.0024441 Training loss after epoch 62: 0.0054856 Training loss after epoch 63: 0.0012796 Training loss after epoch 64: 0.0013482 Training loss after epoch 65: 0.0038288 Training loss after epoch 66: 0.0013217 Training loss after epoch 67: 0.0022817 Training loss after epoch 68: 0.0025086 Training loss after epoch 69: 0.0013634 Training loss after epoch 70: 0.0014228
if progress == "final-loss" plot(1:iteration,lossByIteration) grid on title('Training Loss by Iteration') xlabel("Iteration") ylabel("Loss") end
Test the trained network on the held-out test set. Use a minibatchqueue object with a minibatch size of 32.
miniBatchSize = 32; mbqTest = minibatchqueue(transTest,2,... 'MiniBatchSize',miniBatchSize,... 'MiniBatchFormat', {'CBT','CB'}, ... 'MiniBatchFcn', @processSpeechMB);
Loop over the test set and predict the class labels for each minibatch.
numObservations = numel(adsTest.Files); classes = string(unique(adsTest.Labels)); predictions = []; % Loop over mini-batches while hasdata(mbqTest) % Read mini-batch of data dlX = next(mbqTest); % Make predictions on the minibatch dlYPred = predict(dlnet,dlX); % Determine corresponding classes predBatch = onehotdecode(dlYPred,classes,1); predictions = [predictions predBatch]; end
Evaluate the classification accuracy on the 600 examples in the held-out test set.
accuracy = mean(predictions' == categorical(adsTest.Labels))
accuracy = 0.9883
Test performance is approximately 99%. You can comment out the 1-D convolution layer and retrain the network without the pre-emphasis filter. The test performance without the pre-emphasis filter is also excellent at approximately 96%, but the use of the pre-emphasis filter makes a small improvement. It is noteworthy, that while the use of the learned pre-emphasis filter has only improved the test accuracy slightly, this was achieved by adding only 5 learnable parameters to the network.
To examine the learned pre-emphasis filter, extract the weights of the 1-D convolutional layer. Plot the frequency response. Recall that the sampling frequency of the data is 8 kHz. Because we initialized the filter to a scaled Kronecker delta sequence (allpass filter), we can easily compare the frequency response of the initialized filter with the learned response.
FIRFilter = dlnet.Layers(2).Weights; [H,W] = freqz(FIRFilter,1,[],8000); delta = kronDelta([5 1 1]); Hinit = freqz(delta,1,[],4000); plot(W,20*log10(abs([H Hinit])),'linewidth',2) grid on xlabel('Hz') ylabel('dB') legend('Learned Filter','Initial Filter','Location','SouthEast') title('Learned Pre-emphasis Filter')

This example showed how to learn a pre-emphasis filter as a preprocessing step in a 2-D convolutional network based on short-time Fourier transforms of the signals. The ability of stftLayer to support backpropagation enabled gradient-based optimization of the filter weights inside the deep network. While this resulted in only a small improvement in the performance of the network on the test set, it achieved this improvement with a trivial increase in the number of learnable parameters.
Appendix: Helper Functions
function [out,info] = helperReadData(x,info) % This function is only for use in the "Learn Pre-Emphasis Filter using % Deep Learning" example. It may change or be removed in a % future release. N = numel(x); x = single(x); if N > 8192 x = x(1:8192); elseif N < 8192 pad = 8192-N; prepad = floor(pad/2); postpad = ceil(pad/2); x = [zeros(prepad,1) ; x ; zeros(postpad,1)]; end x = (x-mean(x))./std(x); x = x(:)'; out = {x,info.Label}; end function [dlX,dlY] = processSpeechMB(Xcell,Ycell) % This function is only for use in the "Learn Pre-Emphasis Filter using % Deep Learning" example. It may change or be removed in a % future release. Xcell = cellfun(@(x)reshape(x,1,1,[]),Xcell,'uni',false); dlX = cat(2,Xcell{:}); dlY = cat(2,Ycell{:}); dlY = onehotencode(dlY,1); end function [grads,loss,state] = modelGradSTFT(net,X,T) % This function is only for use in the "Learn Pre-Emphasis Filter using % Deep Learning" example. It may change or be removed in a % future release. [y,state] = net.forward(X); loss = crossentropy(y,T); grads = dlgradient(loss,net.Learnables); loss = double(gather(extractdata(loss))); end
See Also
Apps
Objects
dlarray|dlnetwork|stftLayer(Signal Processing Toolbox) |istftLayer(Signal Processing Toolbox)
Functions
dlstft(Signal Processing Toolbox) |dlistft(Signal Processing Toolbox) |stft(Signal Processing Toolbox) |istft(Signal Processing Toolbox) |stftmag2sig(Signal Processing Toolbox)