Delay
Delay discrete-time input by specified number of samples or frames
Compatibility
Note
The Delay block from the dspsigops library has
been replaced by the Delay (Simulink) block from the Discrete library
in Simulink®. Existing instances of the dspsigops
Delay block will be replaced with Simulink Delay block when there is an exact match in functionality between the
two blocks. For new models, use the Delay block from the Discrete
library in Simulink.
Library
Signal Operations
dspsigops
Description
The Delay block delays a discrete-time input by the number of samples or frames specified in the Delay units and Delay parameters. The Delay value must be an integer value greater than or equal to zero. When you enter a value of zero for the Delay parameter, any initial conditions you might have entered have no effect on the output.
The Delay block allows you to set the initial conditions of the signal that is being delayed. The initial conditions must be numeric.
Frame-Based Processing
When you set the Input processing parameter to
Columns as channels (frame based), the block treats
each column of the M-by-N input matrix as an
independent channel. The block delays each channel of the input as specified by the
Delay parameter.
The Delay parameter can be a scalar integer by which the block equally delays all channels or a vector whose length is equal to the number of channels.
There are four different choices for initial conditions. The initial conditions can be the same or different for each channel. They can also be constant or varying along each channel. See the Frame-Based Processing Examples section for more information.
Sample-Based Processing
When you set the Input processing parameter to
Elements as channels (sample based), the block treats
each element of the N-D input array as an independent channel. Thus, the total
number of channels in the input is equal to the product of the input dimensions. The
dimension of the output is the same as that of the input.
The Delay parameter can be a scalar integer by which to equally delay all channels or an N-D array of the same dimensions as the input array, containing nonnegative integers that specify the number of sample intervals to delay each channel of the input.
There are four different choices for initial conditions. The initial conditions can be the same or different for each channel. They can also be the same or different within a channel. See the Sample-Based Processing Examples section for more information.
Resetting the Delay
The Delay block resets the delay whenever it detects a reset event at the optional
Rst port. The reset sample time must be a positive integer
multiple of the input sample time.
The reset event is specified by the Reset port parameter, and can be one of the following:
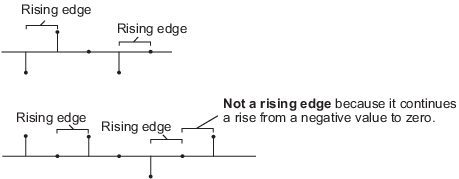
Nonedisables theRstport.Rising edgetriggers a reset operation when theRstinput does one of the following:Rises from a negative value to a positive value or zero
Rises from zero to a positive value, where the rise is not a continuation of a rise from a negative value to zero (see the following figure)
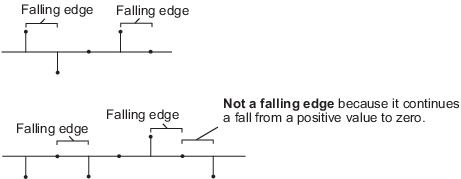
Falling edgetriggers a reset operation when theRstinput does one of the following:Falls from a positive value to a negative value or zero
Falls from zero to a negative value, where the fall is not a continuation of a fall from a positive value to zero (see the following figure)
Either edgetriggers a reset operation when theRstinput isRising edgeorFalling edge(as described earlier).Non-zero sampletriggers a reset operation at each sample time that theRstinput is not zero.
Note
When running simulations in the Simulink MultiTasking mode, reset signals have a one-sample latency. Therefore, when the block detects a reset event, there is a one-sample delay at the reset port rate before the block applies the reset. For more information on latency and the Simulink tasking modes, see Excess Algorithmic Delay (Tasking Latency) and Time-Based Scheduling and Code Generation (Simulink Coder).
This block supports Simulink virtual buses.
Examples
Frame-Based Processing Examples
There are four different choices for initial conditions. The initial conditions can be the same or different for each channel. They can also be constant or varying along each channel. The next sections describe the behavior of the block for each of these four cases:
Case 1 — Use the Same Initial Conditions for Each Channel and Within a Channel
Enter a scalar value for the initial conditions. This value is used as the constant initial condition value for each of the channels.
For example, suppose your input is a matrix and you set the Input
processing parameter to Columns as channels (frame
based).
You want the initial conditions of your three-channel signal to be identical and zero for the first frame:
Set the Delay (frames) parameter to
1.Clear the Specify different initial conditions for each channel and the Specify different initial conditions within a channel check boxes.
Set the Initial conditions parameter to a scalar value of
0.The output of the delay block is
0, the scalar initial condition value, is used across the channels and within the channels for the first frame. This frame is the output at sample time zero.
Case 2 — Use Different Initial Conditions for Each Channel and the Same Initial Conditions Within a Channel
The initial conditions must be a vector of length N, where N ≥ 1. N is also equal to the number of channels in your signal. These initial condition values are used as the constant initial condition value for each of the channels.
For example, suppose your input is a matrix and you set the Input
processing parameter to Columns as channels (frame
based).
You want the initial conditions of your three-channel signal to be [0 10
20] for the first frame:
Set the Delay (frames) parameter to
1.Select the Specify different initial conditions for each channel check box.
Clear the Specify different initial conditions within a channel check box.
Set the Initial conditions parameter to
[0 10 20].The output of the delay block is
The initial condition vector expands to create the frame that is output at sample time zero. Different initial conditions are used for each channel, but the same initial condition value is used with a channel.
Case 3 — Use the Same Initial Conditions for Each Channel and Different Initial Conditions Within a Channel
In this case, the Delay parameter can be a scalar integer by which to equally delay all channels or a vector whose length is equal to the number of channels. All the values of this vector must be equal.
Enter the initial conditions as a vector. These values are used as the initial
condition value along each of the channels to be delayed. The initial condition
vector must have length equal to the value of the Delay
(frames) parameter multiplied by the frame length. For example, if
you want to delay your signal by two frames with frame length two and an initial
condition value of 3, enter your initial condition vector as [3 3 3
3].
For example, suppose your input is a matrix and you set the Input
processing parameter to Columns as channels (frame
based).
You want the initial conditions of your three-channel signal to be the same along each of the channels to be delayed:
Set the Delay (frame) parameter to
1.Clear the Specify different initial conditions for each channel check box.
Select the Specify different initial conditions within a channel check box.
Set the Initial conditions parameter to
[10 20 30].The output of the delay block is
The initial condition vector defines the initial condition values within each of the three channels. The same initial conditions are used for each channel, but different initial condition values are used with a channel.
Case 4 — Use Different Initial Conditions for Each Channel and Within a Channel
Enter a cell array for your initial condition values. Or, when you have a scalar delay value, you can enter the initial conditions as a matrix.
For example, suppose your input is a matrix and you set the Input
processing parameter to Columns as channels (frame
based).
You want the initial conditions of your three-channel signal to be different for each channel and along each channel.
Set the Delay (frames) parameter to
1.Select the Specify different initial conditions for each channel and the Specify different initial conditions within a channel check boxes.
Set the Initial conditions parameter to either
[10 20 30; 40 50 60; 70 80 90]or{[10 40 70];[20 50 80];[30 60 90]}. Each cell of the cell array represents the delay along one channel.Regardless of whether you use a matrix or cell array, the output of the delay block is
The initial condition matrix is the output at sample time zero. The elements of the initial condition cell array define the initial condition values within each channel. The first element, a vector, represents the initial conditions within channel 1. The second element, a vector, represents the initial conditions within channel 2, and so on. Different initial conditions are used for each channel and within the channels.
Sample-Based Processing Examples
There are four different choices for initial conditions. The initial conditions can be the same or different for each channel. They can also be the same or different along each channel. The next sections describe the behavior of the block for each of these four cases:
Case 1 — Use the Same Initial Conditions for Each Channel and Within a Channel
Enter a scalar value for the initial conditions. This value is used as the constant initial condition value for each of the channels.
For example, suppose your input is a matrix and you set the Input
processing parameter to Elements as channels (sample
based).
You want the initial conditions of your four-channel signal to be identical and zero for the first two samples:
Set the Delay (samples) parameter to
2.Clear the Specify different initial conditions for each channel and Specify different initial conditions within a channel check boxes.
Set the Initial conditions parameter to a scalar value of
0.The output of the delay block is
0, the scalar initial condition value, is used for each channel and within the channels. It is the output at sample time zero and sample time one.
Case 2 — Use Different Initial Conditions for Each Channel and the Same Initial Conditions Within a Channel
The initial conditions must be an N-D array for N-D input. The initial conditions must have the same dimensions as the input data. These initial condition values are used as the constant initial condition value for each of the channels.
For example, suppose your input is a matrix and you set the Input
processing parameter to Elements as channels (sample
based).
You want the initial conditions of your four-channel signal to be
for the first two samples:
Set the Delay (samples) parameter to
2.Select the Specify different initial conditions for each channel check box.
Clear the Specify different initial conditions within a channel check box.
Set the Initial conditions parameter to
[7 9; 11 13].The output of the delay block is
The initial condition matrix is the output at sample time zero and sample time one. Different initial conditions are used for each channel; the same initial condition value is used within a channel.
Case 3 — Use the Same Initial Conditions for Each Channel and Different Initial Conditions Within a Channel
In this case, for N-D sample-based inputs, the initial conditions parameter must be a vector whose length is equal to the delay value, specified by the Delay parameter. The values in this vector are used as the initial condition values along each of the channels to be delayed.
For example, suppose your input is a matrix and you set the Input
processing parameter to Elements as channels (sample
based).
You want the initial conditions of your four channel signal to be the same along each of the channels to be delayed:
Set the Delay (samples) parameter to
2.Clear the Specify different initial conditions for each channel check box.
Select the Specify different initial conditions within a channel check box.
Set the Initial conditions parameter to
[10 20].The output of the delay block is
The first element of the initial conditions vector is the output, for all channels, at sample time zero. The second element of the initial conditions vector is the output, for all channels, at sample time one. The same initial conditions are used for each channel, but different initial condition values are used within a channel.
Case 4 — Use Different Initial Conditions for Each Channel and Within a Channel
Enter a cell array for your initial condition values. The cell array must be the same size as your input signal. Each cell of the cell array represents the delay values for one channel, and must be a vector of size equal to the delay value. If you have a vector or scalar input and a scalar delay value, you can enter the initial conditions as a matrix.
For example, suppose your input is a matrix and you set the Input
processing parameter to Elements as channels (sample
based).
You want the initial conditions of your two channel signal to be different for each channel and along each channel:
Set the Delay (samples) parameter to
2.Select the Specify different initial conditions for each channel and Specify different initial conditions within a channel check boxes.
Set the Initial conditions parameter to
[10 20; 30 40].The output of the delay block is
The first row of the initial conditions vector is the output at sample time zero. The second row of the initial conditions vector is the output at sample time one. Different initial conditions are used for each channel and within the channels.
In addition, suppose your input is a matrix and you set the Input
processing parameter to Elements as channels (sample
based).
You want the initial conditions of your two-channel signal to be different for each channel and along each channel:
Set the Delay (samples) parameter to
2.Select the Specify different initial conditions for each channel and the Specify different initial conditions within a channel check boxes.
Set the Initial conditions parameter to
{[11 15] [12 16]; [13 17] [14 18]}. The dimensions of the cell array match the dimensions of the input. Also, each element of the cell array represents the initial conditions within one channel.The output of the delay block is
Each element of the cell array represents the initial conditions within a channel. The first element, a vector, represents the initial conditions within channel 1. The second element, a vector, represents the initial conditions within channel 2, and so on. Different initial conditions are used for each channel and within the channels.
Parameters
- Input processing
Specify how the block should process the input. You can set this parameter to one of the following options:
Columns as channels (frame based)— When you select this option, the block treats each column of the input as a separate channel.Elements as channels (sample based)— When you select this option, the block treats each element of the input as a separate channel.
- Delay units
Select whether you want to delay your input by a specified number of
SamplesorFrames. This parameter appears only when you set the Input processing parameter toColumns as channels (frame based).- Delay (samples) or Delay (frames)
See Sample-Based Processing and Frame-Based Processing for a description of what format to use for each configuration of the block dialog.
- Specify different initial conditions for each channel
Select this check box when you want the initial conditions to vary across the channels. When you do not select this check box, the initial conditions are the same across the channels.
- Specify different initial conditions within a channel
Select this check box when you want the initial conditions to vary within the channels. When you do not select this check box, the initial conditions are the same within the channels.
- Initial conditions
Enter a scalar, vector, matrix, or cell array of initial condition values, depending on your choice for the Specify different initial conditions for each channel and Specify different initial conditions within a channel check boxes. See Sample-Based Processing and Frame-Based Processing for a description of what format to use for each configuration of the block dialog.
- Reset port
Determines the reset event that causes the block to reset the delay. For more information, see Resetting the Delay.
Supported Data Types
Double-precision floating point
Single-precision floating point
Fixed point (signed and unsigned)
Boolean
8-, 16-, and 32-bit signed integers
8-, 16-, and 32-bit unsigned integers
Extended Capabilities
Version History
Introduced before R2006a
See Also
dsp.Delay | Unit Delay (Simulink) | Variable Fractional Delay | Variable Integer Delay (Simulink)
