freqz
Frequency response of filters in channelizer
Description
[
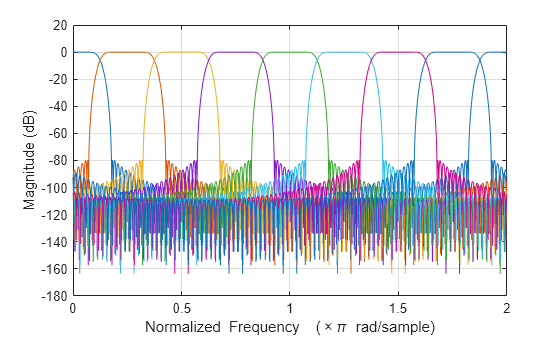
computes a matrix of complex frequency responses for each filter in the H,w] = freqz(obj)dsp.Channelizer
System object™. Each column of H corresponds to the frequency
response for one of the filters in the channelizer. w is a
vector of normalized frequencies at which the rows of H are
computed.
[
computes the frequency response of the filters with indices corresponding to the
elements in the vector H,w] = freqz(obj,ind)ind. ind is a row
vector of indices between 1 and
obj.NumFrequencyBands. By default, this vector is
[1:N], where N is the number of frequency
bands.
For example, to compute the frequency response of the first 4 filters, set
ind to
[1:4].
channelizer = dsp.Channelizer; [H,w] = freqz(channelizer,[1:4]);
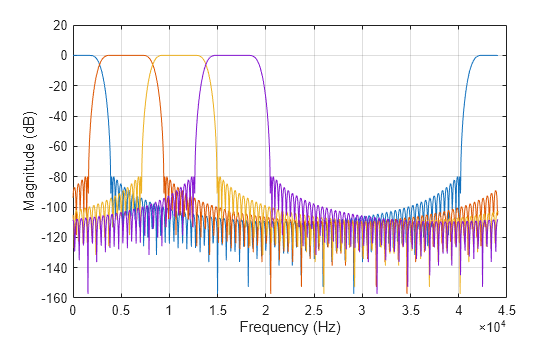
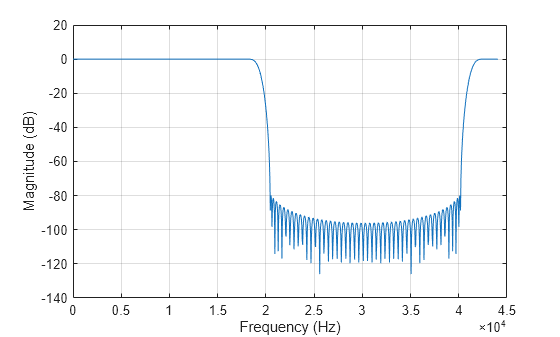
[
computes the frequency response of the filters with additional options specified by
one or more H,f] = freqz(obj,ind,Name,Value)Name,Value pair arguments.
For example, to specify a sampling rate of 44100 Hz, set 'Fs'
to 44100. To compute the frequency response using 1024 frequency
points, set 'NFFT' to 1024. In addition, to
compute the sum of the frequency response of the filters, set
'overall' to
true.
channelizer = dsp.Channelizer; [H,f] = freqz(channelizer,[1:4],'Fs',44100,'NFFT',1024,'overall',true);
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Version History
Introduced in R2017b