Group Delay Estimation in Simulink
This example shows how to estimate the group delay of a filter in Simulink®.
To estimate the group delay of the filter, extract the phase response and compute its negative derivative with respect to frequency. Group delay is defined as  .
.
The Example Model
The Simulink model GroupDelayEstimator estimates the group delay of the given filter using the following blocks:
Discrete Transfer Function Estimator - Estimate the discrete transfer function of the filter using its input and output.
Phase Extractor - Extracts the phase response from the filter transfer function estimate.
Gain (Simulink) - Scales the phase response to denormalize frequency to 0 to half the sample-rate. In this case sample-rate is set to 44.1kHz. Negative of this value is used for estimating the group delay in number of samples.
Differentiator Filter - Takes the derivative of the phase with respect to frequency.
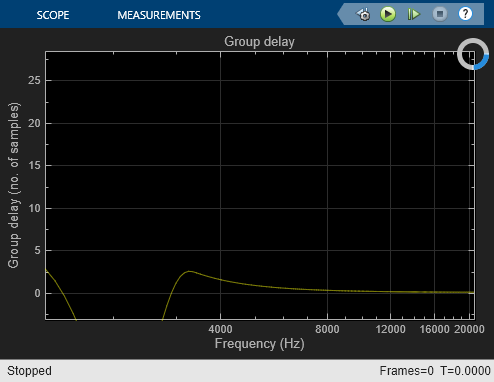
Array Plot - View the group delay of the filter in number of samples.

The Filter Selector block will allow you to choose from different filters. The group delay estimator output is noisy. To filter the noise the output of the estimator is passed through a low pass filter so that the estimated group delay can be smoothly visualized. This lowpass filter has a group delay which is equal to half the filter order. Hence initial few samples are dropped to compensate for this group delay.
Exploring the Example
Open and run the model. You can see the group delay of the selected filter in number of samples in the Array Plot block. The theoretical value for a linear phase FIR Filter block is half the order of the filter. For Biquad filter and Notch filter the theoretical group delay can be visualized by opening the block mask and clicking the View Filter Response button. For Notch filter block, you can tune the notch frequency and see the group delay change accordingly.

The Lowpass filter block after the group delay estimator is used to smooth the estimate. Tune the cutoff frequency of this filter and notice the noise in the estimated group delay.
See Also
Blocks
- Discrete Transfer Function Estimator | Phase Extractor | Gain (Simulink) | Differentiator Filter | Array Plot | Biquad Filter | Lowpass Filter