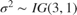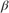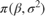customblm
Bayesian linear regression model with custom joint prior distribution
Description
The Bayesian linear regression
model object customblm contains a log of the pdf of the
joint prior distribution of
(β,σ2). The log pdf
is a custom function that you declare.
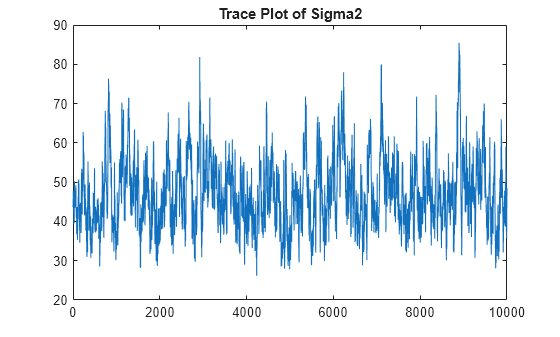
The data likelihood is where ϕ(yt;xtβ,σ2) is the Gaussian probability density evaluated at yt with mean xtβ and variance σ2. MATLAB® treats the prior distribution function as if it is unknown. Therefore, the resulting posterior distributions are not analytically tractable. To estimate or simulate from posterior distributions, MATLAB implements the slice sampler.
In general, when you create a Bayesian linear regression model object, it specifies the joint prior distribution and characteristics of the linear regression model only. That is, the model object is a template intended for further use. Specifically, to incorporate data into the model for posterior distribution analysis, pass the model object and data to the appropriate object function.
Creation
Syntax
Description
PriorMdl = customblm(NumPredictors,'LogPDF',LogPDF)PriorMdl) composed of
NumPredictors predictors and an intercept, and sets
the NumPredictors property. LogPDF
is a function representing the log of the joint prior distribution of
(β,σ2).
PriorMdl is a template that defines the prior
distributions and the dimensionality of β.
PriorMdl = customblm(NumPredictors,'LogPDF',LogPDF,Name,Value)NumPredictors) using name-value pair arguments.
Enclose each property name in quotes. For example,
customblm(2,'LogPDF',@logprior,'Intercept',false)
specifies the function that represents the log of the joint prior density of
(β,σ2),
and specifies a regression model with 2 regression coefficients, but no
intercept.
Properties
Object Functions
estimate | Estimate posterior distribution of Bayesian linear regression model parameters |
simulate | Simulate regression coefficients and disturbance variance of Bayesian linear regression model |
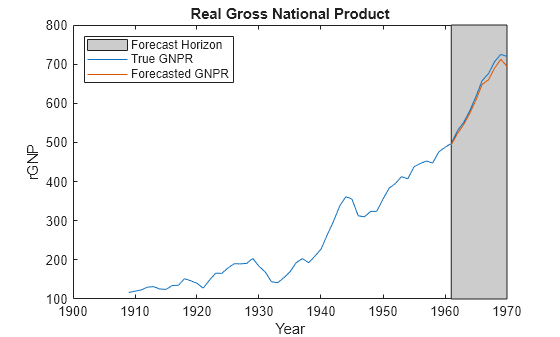
forecast | Forecast responses of Bayesian linear regression model |
plot | Visualize prior and posterior densities of Bayesian linear regression model parameters |
summarize | Distribution summary statistics of standard Bayesian linear regression model |
Examples
More About
Alternatives
The bayeslm function can create any supported prior model object for Bayesian linear regression.
Version History
Introduced in R2017a
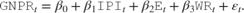

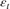

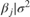
![${\left[ {\begin{array}{*{20}{c}} { - 25}&4&0&3 \end{array}} \right]^\prime }$](../examples/econ/win64/CreateCustomMultivariatetPriorModelForCoefficientsExample_eq06094370667326100457.png)
![${\left[ {\begin{array}{*{20}{c}} {1}&1&1&1 \end{array}} \right]^\prime }$](../examples/econ/win64/CreateCustomMultivariatetPriorModelForCoefficientsExample_eq17422027603262012745.png)