bayeslm
Create Bayesian linear regression model object
Syntax
Description
PriorMdl = bayeslm(NumPredictors)PriorMdl is
a template that defines the prior distributions and dimensionality of
β.
PriorMdl = bayeslm(NumPredictors,ModelType=modelType)modelType for
β and σ2. For
this syntax, modelType can be:
'conjugate','semiconjugate', or'diffuse'to create a standard Bayesian linear regression prior model'mixconjugate','mixsemiconjugate', or'lasso'to create a Bayesian linear regression prior model for predictor variable selection
For example, ModelType="conjugate" specifies
conjugate priors for the Gaussian likelihood, that is,
β|σ2 as
Gaussian, σ2 as inverse gamma.
PriorMdl = bayeslm(NumPredictors,ModelType=modelType,Name=Value)modelType.
If you specify
ModelType="empirical", you must also specify theBetaDrawsandSigma2Drawsname-value arguments.BetaDrawsandSigma2Drawscharacterize the respective prior distributions.If you specify
ModelType="custom", you must also specify theLogPDFname-value argument.LogPDFcompletely characterizes the joint prior distribution.
Examples
Consider the multiple linear regression model that predicts the US real gross national product (GNPR) using a linear combination of industrial production index (IPI), total employment (E), and real wages (WR).
For all , is a series of independent Gaussian disturbances with a mean of 0 and variance .
Suppose that the regression coefficients and the disturbance variance are random variables, and their prior values and distribution are unknown. In this case, use the noninformative Jefferys prior: the joint prior distribution is proportional to .
These assumptions and the data likelihood imply an analytically tractable posterior distribution.
Create a diffuse prior model for the linear regression parameters, which is the default model type. Specify the number of predictors p.
p = 3; Mdl = bayeslm(p)
Mdl =
diffuseblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
| Mean Std CI95 Positive Distribution
-----------------------------------------------------------------------------
Intercept | 0 Inf [ NaN, NaN] 0.500 Proportional to one
Beta(1) | 0 Inf [ NaN, NaN] 0.500 Proportional to one
Beta(2) | 0 Inf [ NaN, NaN] 0.500 Proportional to one
Beta(3) | 0 Inf [ NaN, NaN] 0.500 Proportional to one
Sigma2 | Inf Inf [ NaN, NaN] 1.000 Proportional to 1/Sigma2
Mdl is a diffuseblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance. bayeslm displays a summary of the prior distributions at the command line. Because the prior is noninformative and the model does not contain data, the summary is trivial.
If you have data, then you can estimate characteristics of the posterior distribution by passing the prior model Mdl and data to estimate.
Consider the linear regression model in Default Diffuse Prior Model. Assume these prior distributions:
. is a 4-by-1 vector of means, and is a scaled 4-by-4 positive definite covariance matrix.
. and are the shape and scale, respectively, of an inverse gamma distribution.
These assumptions and the data likelihood imply a normal-inverse-gamma semiconjugate model. The conditional posteriors are conjugate to the prior with respect to the data likelihood, but the marginal posterior is analytically intractable.
Create a normal-inverse-gamma semiconjugate prior model for the linear regression parameters. Specify the number of predictors p.
p = 3;
Mdl = bayeslm(p,ModelType="semiconjugate") Mdl =
semiconjugateblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
Mu: [4×1 double]
V: [4×4 double]
A: 3
B: 1
| Mean Std CI95 Positive Distribution
-------------------------------------------------------------------------------
Intercept | 0 100 [-195.996, 195.996] 0.500 N (0.00, 100.00^2)
Beta(1) | 0 100 [-195.996, 195.996] 0.500 N (0.00, 100.00^2)
Beta(2) | 0 100 [-195.996, 195.996] 0.500 N (0.00, 100.00^2)
Beta(3) | 0 100 [-195.996, 195.996] 0.500 N (0.00, 100.00^2)
Sigma2 | 0.5000 0.5000 [ 0.138, 1.616] 1.000 IG(3.00, 1)
Mdl is a semiconjugateblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance. bayeslm displays a summary of the prior distributions at the command line. For example, the elements of Positive represent the prior probability that the corresponding parameter is positive.
If you have data, then you can estimate characteristics of the marginal or conditional posterior distribution by passing the prior model Mdl and data to estimate.
Consider the linear regression model in Default Diffuse Prior Model. Assume these prior distributions:
. is a 4-by-1 vector of means, and is a scaled 4-by-4 positive definite covariance matrix. Suppose you have prior knowledge that and V is the identity matrix.
. and are the shape and scale, respectively, of an inverse gamma distribution.
These assumptions and the data likelihood imply a normal-inverse-gamma conjugate model.
Create a normal-inverse-gamma conjugate prior model for the linear regression parameters. Specify the number of predictors p and set the regression coefficient names to the corresponding variable names.
p = 3; Mdl = bayeslm(p,ModelType="conjugate",Mu=[-20; 4; 0.1; 2],V=eye(4), ... VarNames=["IPI" "E" "WR"])
Mdl =
conjugateblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
Mu: [4×1 double]
V: [4×4 double]
A: 3
B: 1
| Mean Std CI95 Positive Distribution
----------------------------------------------------------------------------------
Intercept | -20 0.7071 [-21.413, -18.587] 0.000 t (-20.00, 0.58^2, 6)
IPI | 4 0.7071 [ 2.587, 5.413] 1.000 t (4.00, 0.58^2, 6)
E | 0.1000 0.7071 [-1.313, 1.513] 0.566 t (0.10, 0.58^2, 6)
WR | 2 0.7071 [ 0.587, 3.413] 0.993 t (2.00, 0.58^2, 6)
Sigma2 | 0.5000 0.5000 [ 0.138, 1.616] 1.000 IG(3.00, 1)
Mdl is a conjugateblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance. bayeslm displays a summary of the prior distributions at the command line. Although bayeslm assigns names to the intercept and disturbance variance, all other coefficients have the specified names.
By default, bayeslm sets the shape and scale to 3 and 1, respectively. Suppose you have prior knowledge that the shape and scale are 5 and 2.
Set the prior shape and scale of to their assumed values.
Mdl.A = 5; Mdl.B = 2
Mdl =
conjugateblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
Mu: [4×1 double]
V: [4×4 double]
A: 5
B: 2
| Mean Std CI95 Positive Distribution
----------------------------------------------------------------------------------
Intercept | -20 0.3536 [-20.705, -19.295] 0.000 t (-20.00, 0.32^2, 10)
IPI | 4 0.3536 [ 3.295, 4.705] 1.000 t (4.00, 0.32^2, 10)
E | 0.1000 0.3536 [-0.605, 0.805] 0.621 t (0.10, 0.32^2, 10)
WR | 2 0.3536 [ 1.295, 2.705] 1.000 t (2.00, 0.32^2, 10)
Sigma2 | 0.1250 0.0722 [ 0.049, 0.308] 1.000 IG(5.00, 2)
bayeslm updates the prior distribution summary based on the changes in the shape and scale.
Consider the linear regression model in Default Diffuse Prior Model. Assume these prior distributions:
 is 4-D t distribution with 50 degrees of freedom for each component and the identity matrix for the correlation matrix. Also, the distribution is centered at
is 4-D t distribution with 50 degrees of freedom for each component and the identity matrix for the correlation matrix. Also, the distribution is centered at ![${\left[ {\begin{array}{*{20}{c}} { - 25}&4&0&3 \end{array}} \right]^\prime }$](../examples/econ/win64/CustomMultivariatetPriorModelForCoefficientsExample_eq06094370667326100457.png) and each component is scaled by the corresponding elements of the vector
and each component is scaled by the corresponding elements of the vector ![${\left[ {\begin{array}{*{20}{c}} {10}&1&1&1 \end{array}} \right]^\prime }$](../examples/econ/win64/CustomMultivariatetPriorModelForCoefficientsExample_eq11954731508684699991.png) .
.
 .
.
bayeslm treats these assumptions and the data likelihood as if the corresponding posterior is analytically intractable.
Declare a MATLAB® function that:
Accepts values of
 and
and 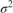 together in a column vector, and accepts values of the hyperparameters
together in a column vector, and accepts values of the hyperparametersReturns the value of the joint prior distribution,
 , given the values of
, given the values of  and
and 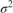
function logPDF = priorMVTIG(params,ct,st,dof,C,a,b) %priorMVTIG Log density of multivariate t times inverse gamma % priorMVTIG passes params(1:end-1) to the multivariate t density % function with dof degrees of freedom for each component and positive % definite correlation matrix C. priorMVTIG returns the log of the product of % the two evaluated densities. % % params: Parameter values at which the densities are evaluated, an % m-by-1 numeric vector. % % ct: Multivariate t distribution component centers, an (m-1)-by-1 % numeric vector. Elements correspond to the first m-1 elements % of params. % % st: Multivariate t distribution component scales, an (m-1)-by-1 % numeric (m-1)-by-1 numeric vector. Elements correspond to the % first m-1 elements of params. % % dof: Degrees of freedom for the multivariate t distribution, a % numeric scalar or (m-1)-by-1 numeric vector. priorMVTIG expands % scalars such that dof = dof*ones(m-1,1). Elements of dof % correspond to the elements of params(1:end-1). % % C: Correlation matrix for the multivariate t distribution, an % (m-1)-by-(m-1) symmetric, positive definite matrix. Rows and % columns correspond to the elements of params(1:end-1). % % a: Inverse gamma shape parameter, a positive numeric scalar. % % b: Inverse gamma scale parameter, a positive scalar. % beta = params(1:(end-1)); sigma2 = params(end); tVal = (beta - ct)./st; mvtDensity = mvtpdf(tVal,C,dof); igDensity = sigma2^(-a-1)*exp(-1/(sigma2*b))/(gamma(a)*b^a); logPDF = log(mvtDensity*igDensity); end
Create an anonymous function that operates like priorMVTIG, but accepts the parameter values only and holds the hyperparameter values fixed.
dof = 50; C = eye(4); ct = [-25; 4; 0; 3]; st = [10; 1; 1; 1]; a = 3; b = 1; prior = @(params)priorMVTIG(params,ct,st,dof,C,a,b);
Create a custom joint prior model for the linear regression parameters. Specify the number of predictors p. Also, specify the function handle for priorMVTIG, and pass the hyperparameter values.
p = 3;
Mdl = bayeslm(p,ModelType="custom",LogPDF=prior)
Mdl =
customblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
LogPDF: @(params)priorMVTIG(params,ct,st,dof,C,a,b)
The priors are defined by the function:
@(params)priorMVTIG(params,ct,st,dof,C,a,b)
Mdl is a customblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance. In this case, bayeslm does not display a summary of the prior distributions at the command line.
Consider the linear regression model in Default Diffuse Prior Model.
Assume these prior distributions:
For k = 0,...,3, has a Laplace distribution with a mean of 0 and a scale of , where is the shrinkage parameter. The coefficients are conditionally independent.
. and are the shape and scale, respectively, of an inverse gamma distribution.
Create a prior model for Bayesian linear regression by using bayeslm. Specify the number of predictors p and the variable names.
p = 3; PriorMdl = bayeslm(p,ModelType="lasso", ... VarNames=["IPI" "E" "WR"]);
PriorMdl is a lassoblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance. By default, bayeslm attributes a shrinkage of 0.01 to the intercept and 1 to the other coefficients in the model.
Using dot notation, change the default shrinkages for all coefficients, except the intercept, by specifying a 3-by-1 vector containing the new values for the Lambda property of PriorMdl.
Attribute a shrinkage of
10toIPIandWR.Because
Ehas a scale that is several orders of magnitude larger than the other variables, attribute a shrinkage of1e5to it.
Lambda(2:end) contains the shrinkages of the coefficients corresponding to the specified variables in the VarNames property of PriorMdl.
PriorMdl.Lambda = [10; 1e5; 10];
Load the Nelson-Plosser data set. Create variables for the response and predictor series.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,"GNPR"};
Perform Bayesian lasso regression by passing the prior model and data to estimate, that is, by estimating the posterior distribution of and . Bayesian lasso regression uses Markov chain Monte Carlo (MCMC) to sample from the posterior. For reproducibility, set a random seed.
rng(1); PosteriorMdl = estimate(PriorMdl,X,y);
Method: lasso MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
-------------------------------------------------------------------------
Intercept | -1.3472 6.8160 [-15.169, 11.590] 0.427 Empirical
IPI | 4.4755 0.1646 [ 4.157, 4.799] 1.000 Empirical
E | 0.0001 0.0002 [-0.000, 0.000] 0.796 Empirical
WR | 3.1610 0.3136 [ 2.538, 3.760] 1.000 Empirical
Sigma2 | 60.1452 11.1180 [42.319, 85.085] 1.000 Empirical
Plot the posterior distributions.
plot(PosteriorMdl)

Given a shrinkage of 10, the distribution of E is fairly dense around 0. Therefore, E might not be an important predictor.
Input Arguments
Number of predictor variables in the Bayesian multiple linear regression model, specified as a nonnegative integer.
NumPredictors must be the same as the number of columns in your predictor data, which you specify during model estimation or simulation.
When counting the number of predictors in the model, exclude the intercept
term specified by Intercept. If you include a column of
ones in the predictor data for an intercept term, then count it as a
predictor variable and specify Intercept=false.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: ModelType="conjugate",Mu=1:3,V=1000*eye(3),A=1,B=0.5
specifies that the prior distribution of Beta given
Sigma2 is Gaussian with mean vector 1:3
and covariance matrix Sigma2*1000*eye(3), and the distribution of
Sigma2 is inverse gamma with shape 1 and
scale 0.5.
Options for All Prior Distributions
Joint prior distribution of (β,σ2), specified as a value in the following tables.
For a standard Bayesian regression model, choose a value in this table.
| Value | Description |
|---|---|
'conjugate' | Normal-inverse-gamma conjugate model
You can adjust corresponding
hyperparameters using the |
'semiconjugate' | Normal-inverse-gamma semiconjugate model
You can adjust corresponding
hyperparameters using the |
'diffuse' | Diffuse prior distributions
|
'empirical' | Custom prior distributions
|
'custom' | Custom prior distributions
|
For a Bayesian regression model that performs predictor variable selection, choose a value in this table.
| Value | Description |
|---|---|
'mixconjugate' | Stochastic search variable selection (SSVS) [1] conjugate prior distributions
For more details, see |
'mixsemiconjugate' | SSVS [1] semiconjugate prior distributions
For more details, see |
'lasso' | Bayesian lasso regression prior distributions [3]
|
The prior model type that you choose depends on your assumptions on the joint distribution of the parameters. Your choice can affect posterior estimates and inferences. For more details, see Implement Bayesian Linear Regression.
Example: ModelType="conjugate"
Data Types: char
Flag for including a regression model intercept, specified as a value in this table.
| Value | Description |
|---|---|
false | Exclude an intercept from the regression model. Therefore, β is a p-dimensional vector, where p is the value of NumPredictors. |
true | Include an intercept in the regression model. Therefore, β is a (p + 1)-dimensional vector. This specification causes a T-by-1 vector of ones to be prepended to the predictor data during estimation and simulation. |
If you include a column of ones in the predictor data for
an intercept term, then specify
Intercept=false.
Example: Intercept=false
Predictor variable names for displays, specified as a string vector or
cell vector of character vectors. VarNames must
contain NumPredictors elements.
VarNames( is the
name of the variable in column j)j of the
predictor data set, which you specify during estimation, simulation, or
forecasting.
The default is {'Beta(1)','Beta(2)',...,'Beta(, where p)'}p is the value of NumPredictors.
Note
You cannot set the name of the intercept or disturbance variance. In displays, bayeslm gives the intercept the name Intercept and the disturbance variance the name Sigma2. Therefore, you cannot use "Intercept" and "Sigma2" as predictor names.
Example: VarNames=["UnemploymentRate";
"CPI"]
Data Types: string | cell | char
Options for Conjugate and Semiconjugate Joint Prior Distribution of β
Mean hyperparameter of the Gaussian prior on β, specified as a numeric vector.
If Mu is a vector, then it must have NumPredictors or NumPredictors + 1 elements.
For
NumPredictorselements,bayeslmsets the prior mean of theNumPredictorspredictors only. Predictors correspond to the columns in the predictor data (specified during estimation, simulation, or forecasting).bayeslmignores the intercept in the model, that is,bayeslmspecifies the default prior mean to any intercept.For
NumPredictors + 1elements, the first element corresponds to the prior mean of the intercept, and all other elements correspond to the predictors.
Example: Mu=[1; 0.08; 2]
Data Types: double
Conditional covariance matrix hyperparameter of the Gaussian prior on
β, specified as a
c-by-c
symmetric, positive definite matrix. c can be
NumPredictors or NumPredictors +
1.
If
cisNumPredictors, thenbayeslmsets the prior covariance matrix tobayeslmattributes the default prior covariances to the intercept, and attributesVto the coefficients of the predictor variables in the data. Rows and columns ofVcorrespond to columns (variables) in the predictor data.If
cisNumPredictors + 1, thenbayeslmsets the entire prior covariance toV. The first row and column correspond to the intercept. All other rows and columns correspond to the columns in the predictor data.
The default value is a flat prior. For an
adaptive prior, specify diag(Inf(Intercept +
NumPredictors,1)). Adaptive priors indicate zero precision in order for the
prior distribution to have as little influence as possible on the posterior
distribution.
For ModelType=conjugate, V is
the prior covariance of β up to a factor of
σ2.
Example: V=diag(Inf(3,1))
Data Types: double
Options for Bayesian Lasso Regression
Lasso regularization parameter for all regression coefficients,
specified as a positive numeric scalar or
(Intercept +
NumPredictors)-by-1 positive numeric vector. Larger
values of Lambda cause corresponding coefficients to
shrink closer to zero.
Suppose X is a T-by-NumPredictors matrix of predictor data, which you specify during estimation, simulation, or forecasting.
If
Lambdais a vector andInterceptistrue,Lambda(1)is the shrinkage for the intercept,Lambda(2)is the shrinkage for the coefficient of the first predictorX(:,1),Lambda(3)is the shrinkage for the coefficient of the second predictorX(:,2),…, andLambda(NumPredictors + 1)is the shrinkage for the coefficient of the last predictorX(:,NumPredictors).If
Lambdais a vector andInterceptisfalse,Lambda(1)is the shrinkage for the coefficient of the first predictorX(:,1),…, andLambda(NumPredictors)is the shrinkage for the coefficient of the last predictorX(:,NumPredictors).If you supply the scalar
sforLambda, then all coefficients of the predictors inXhave a shrinkage ofs.If
Interceptistrue, the intercept has a shrinkage of0.01, andlassoblmstores[0.01; s*ones(NumPredictors,1)]inLambda.Otherwise,
lassoblmstoress*ones(NumPredictors,1)inLambda.
Example: Lambda=6
Data Types: double
Options for Prior Distribution of β and γ for SSVS Predictor Variable Selection
Component-wise mean hyperparameter of the Gaussian mixture prior on
β, specified as an (Intercept + NumPredictors)-by-2 numeric
matrix. The first column contains the prior means for component 1 (the variable-inclusion
regime, that is, γ = 1). The second column contains the prior means for
component 2 (the variable-exclusion regime, that is, γ = 0).
If
Interceptisfalse, thenMuhasNumPredictorsrows.bayeslmsets the prior mean of theNumPredictorscoefficients corresponding to the columns in the predictor data set, which you specify during estimation, simulation, or forecasting.Otherwise,
MuhasNumPredictors + 1elements. The first element corresponds to the prior means of the intercept, and all other elements correspond to the predictor variables.
Tip
To perform SSVS, use the default value of Mu.
Data Types: double
Component-wise variance factor or variance hyperparameter of the
Gaussian mixture prior on β, specified an (Intercept + NumPredictors)-by-2 positive
numeric matrix. The first column contains the prior variance factors for component 1 (the
variable-inclusion regime, that is, γ = 1). The second column contains the
prior variance factors for component 2 (the variable-exclusion regime, that is,
γ = 0). For conjugate models
(ModelType="mixconjugate"), V
contains variance factors, and for semiconjugate models
(ModelType="mixsemiconjugate"),
V contains variances.
If
Interceptisfalse, thenVhasNumPredictorsrows.bayeslmsets the prior variance factor of theNumPredictorscoefficients corresponding to the columns in the predictor data set, which you specify during estimation, simulation, or forecasting.Otherwise,
VhasNumPredictors + 1elements. The first element corresponds to the prior variance factor of the intercept, and all other elements correspond to the predictor variables.
Tip
To perform SSVS, specify a larger variance factor for regime 1 than for regime 2. That is, for all
j, specifyV(>j,1)V(.j,2)For details on what value to specify for
V, see [1].
Data Types: double
Prior probability distribution for the variable inclusion and
exclusion regimes, specified an (Intercept +
NumPredictors)-by-1 numeric vector of values in [0,1], or a function
handle in the form @fcnName, where fcnName is the function
name. Probability represents the prior probability distribution of
γ =
{γ1,…,γK},
where:
K =
Intercept+NumPredictors, which is the number of coefficients in the regression model.γk ∈ {0,1} for k = 1,…,K. Therefore, the sample space has a cardinality of 2K.
γk = 1 indicates variable
VarNames(is included in the model, and γk = 0 indicates that the variable is excluded from the model.k)
If Probability is a numeric vector:
Rows correspond to the variable names in
VarNames. For models containing an intercept, the prior probability for intercept inclusion isProbability(1).For
kkProbability(k).Prior probabilities of the variable-inclusion regime, among all variables and the intercept, are independent.
If Probability is a function handle, then it represents a custom prior distribution of the variable-inclusion regime probabilities. The corresponding function must have this declaration statement (the argument and function names can vary):
logprob = regimeprior(varinc)
logprobis a numeric scalar representing the log of the prior distribution. You can write the prior distribution up to a proportionality constant.varincis a K-by-1 logical vector. Elements correspond to the variable names inVarNamesand indicate the regime in which the corresponding variable exists.varinc(=k)trueindicatesVarName(is included in the model, andk)varinc(=k)falseindicates it is excluded from the model.
You can include more input arguments, but they must be known when you call
bayeslm.
For details on what value to specify for Probability, see [1].
Data Types: double | function_handle
Prior correlation matrix of β for both components in the mixture model, specified as
an (Intercept +
NumPredictors)-by-(Intercept +
NumPredictors) numeric, positive definite matrix. Consequently, the
prior covariance matrix for component j
For conjugate (
ModelType="mixconjugate"),sigma2*diag(sqrt(V(:,j)))*Correlation*diag(sqrt(V(:,j)))For semiconjugate (
ModelType="mixsemiconjugate"),diag(sqrt(V(:,j)))*Correlation*diag(sqrt(V(:,j)))
where sigma2 is σ2 and V is the matrix of coefficient variance factors or variances.
Rows and columns correspond to the variable names in VarNames.
By default, regression coefficients are uncorrelated, conditional on the regime.
Note
You can supply any appropriately sized numeric matrix. However, if your specification is not
positive definite, bayeslm issues a warning and replaces your
specification with CorrelationPD,
where:
CorrelationPD = 0.5*(Correlation + Correlation.');
Tip
For details on what value to specify for Correlation, see [1].
Data Types: double
Options for Prior Distribution of σ2
Shape hyperparameter of the inverse gamma prior on σ2, specified a numeric scalar.
A must be at least –(Intercept +
NumPredictors)/2.
With B held fixed, the inverse gamma distribution becomes taller and more
concentrated as A increases. This characteristic weighs the prior model
of σ2 more heavily than the likelihood during
posterior estimation.
For the functional form of the inverse gamma distribution, see Analytically Tractable Posteriors.
This option does not apply to empirical or custom prior distributions.
Example: A=0.1
Data Types: double
Scale hyperparameter of the inverse gamma prior on
σ2, specified as a
positive scalar or Inf.
With A held fixed, the inverse gamma distribution becomes taller and more
concentrated as B increases. This characteristic weighs the prior model
of σ2 more heavily than the likelihood during
posterior estimation.
This option does not apply to empirical or custom prior distributions.
Example: B=5
Data Types: double
Required Options for Empirical Joint Prior Distributions
Random sample from the prior distribution of β,
specified as an (Intercept +
NumPredictors)-by-NumDraws
numeric matrix. Rows correspond to regression coefficients: the first
row corresponds to the intercept, and the subsequent rows correspond to
columns in the predictor data. Columns correspond to successive draws
from the prior distribution.
BetaDraws and Sigma2Draws must have the same number of columns.
For best results, draw a large number of samples.
Data Types: double
Random sample from the prior distribution of
σ2, specified as a
1-by-NumDraws numeric row vector. Columns
correspond to successive draws from the prior distribution.
BetaDraws and Sigma2Draws must have the same number of columns.
For best results, draw a large number of samples.
Data Types: double
Required Options for Custom Prior Distributions
Log of the joint probability density function of (β,σ2), specified as a function handle.
Suppose logprior is
the name of the MATLAB® function defining the joint prior distribution of
(β,σ2). Then,
logprior must have this form.
function [logpdf,glpdf] = logprior(params) ... end
logpdfis a numeric scalar representing the log of the joint probability density of (β,σ2).glpdfis an (Intercept+NumPredictors+ 1)-by-1 numeric vector representing the gradient oflogpdf. Elements correspond to the elements ofparams.glpdfis an optional output argument, and only the Hamiltonian Monte Carlo sampler (seehmcSampler) applies it. If you know the analytical partial derivative with respect to some parameters, but not others, then set the elements ofglpdfcorresponding to the unknown partial derivatives toNaN. MATLAB computes the numerical gradient for missing partial derivatives, which is convenient, but slows sampling.paramsis an (Intercept+NumPredictors+ 1)-by-1 numeric vector. The firstIntercept+NumPredictorselements must correspond to values of β, and the last element must correspond to the value of σ2. The first element of β is the intercept, if one exists. All other elements correspond to predictor variables in the predictor data, which you specify during estimation, simulation, or forecasting.
Example: LogPDF=@logprior
Output Arguments
Bayesian linear regression model storing prior model assumptions, returned as an object in this table.
Value of ModelType | Returned Bayesian Linear Regression Model Object |
|---|---|
'conjugate' | conjugateblm |
'semiconjugate' | semiconjugateblm |
'diffuse' | diffuseblm |
'empirical' | empiricalblm |
'custom' | customblm |
'mixconjugate' | mixconjugateblm |
'mixsemiconjugate' | mixsemiconjugateblm |
'lasso' | lassoblm |
PriorMdl specifies the joint prior distribution and characteristics of the linear regression model only. The model object is a template intended for further use. To incorporate data into the model for posterior distribution analysis, pass the model object and data to the appropriate object function, for example, estimate or simulate.
More About
A Bayesian linear regression model treats the parameters β and σ2 in the multiple linear regression (MLR) model yt = xtβ + εt as random variables.
For times t = 1,...,T:
yt is the observed response.
xt is a 1-by-(p + 1) row vector of observed values of p predictors. To accommodate a model intercept, x1t = 1 for all t.
β is a (p + 1)-by-1 column vector of regression coefficients corresponding to the variables that compose the columns of xt.
εt is the random disturbance with a mean of zero and Cov(ε) = σ2IT×T, while ε is a T-by-1 vector containing all disturbances. These assumptions imply that the data likelihood is
ϕ(yt;xtβ,σ2) is the Gaussian probability density with mean xtβ and variance σ2 evaluated at yt;.
Before considering the data, you impose a joint prior distribution assumption on (β,σ2). In a Bayesian analysis, you update the distribution of the parameters by using information about the parameters obtained from the likelihood of the data. The result is the joint posterior distribution of (β,σ2) or the conditional posterior distributions of the parameters.
References
[1] George, E. I., and R. E. McCulloch. "Variable Selection Via Gibbs Sampling." Journal of the American Statistical Association. Vol. 88, No. 423, 1993, pp. 881–889.
[2] Koop, G., D. J. Poirier, and J. L. Tobias. Bayesian Econometric Methods. New York, NY: Cambridge University Press, 2007.
[3] Park, T., and G. Casella. "The Bayesian Lasso." Journal of the American Statistical Association. Vol. 103, No. 482, 2008, pp. 681–686.
Version History
Introduced in R2017a
See Also
Objects
conjugateblm|semiconjugateblm|diffuseblm|customblm|empiricalblm|lassoblm|mixconjugateblm|mixsemiconjugateblm
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)