cusumtest
Cusum test for structural change
Syntax
Description
h = cusumtest(Tbl)ResponseVariable name-value
argument. To select different predictor variables, use the
PredictorNames name-value argument.
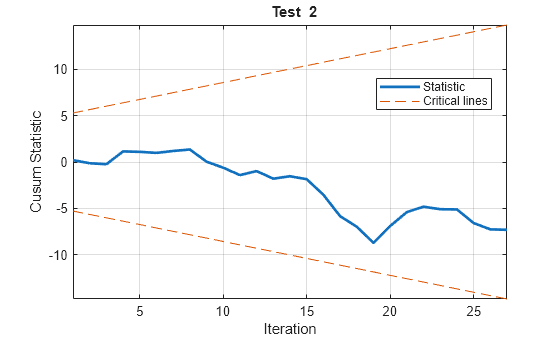
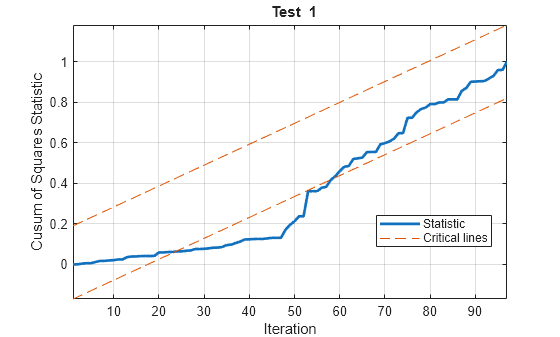
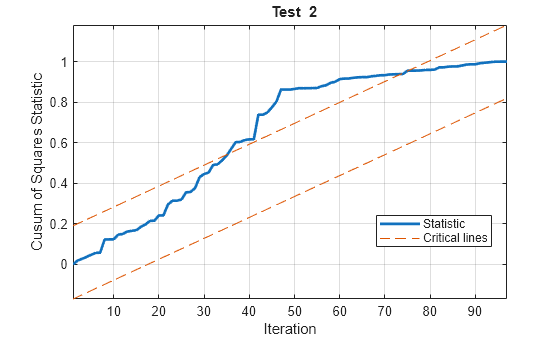
h = cusumtest(___,Name=Value)cusumtest conducts multiple tests:
cusumtesttreats each test as separate from all other tests.All outputs expand their singleton dimension to contain results from each test.
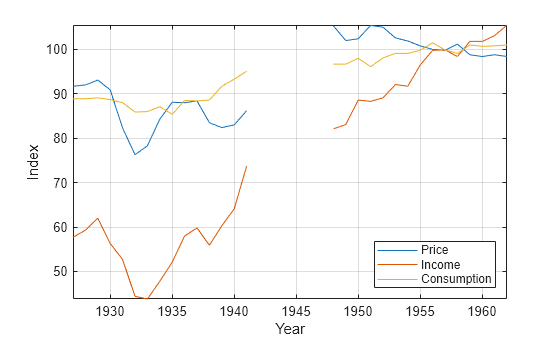
For example, cusumtest(Tbl,ResponseVariable="RGDP",Test=["cusum"
cusumsq"]) conducts two cusum tests using GDP
as the response variable in the regressions and all other variables in the table
Tbl as predictors. The first test uses the cusum test
statistic and the second test uses the cusum of squares test statistic.
[
also returns the following decision statistics from conducting a cusum test,
using any input-argument combination in the previous syntaxes:h,H,Stat,W,B]
= cusumtest(___)
h, the test decisionH, the sequence of decisions for each iteration of the testStat, the sequence of test statisticsW, the sequence of recursive residualsB, the sequence of coefficient estimates
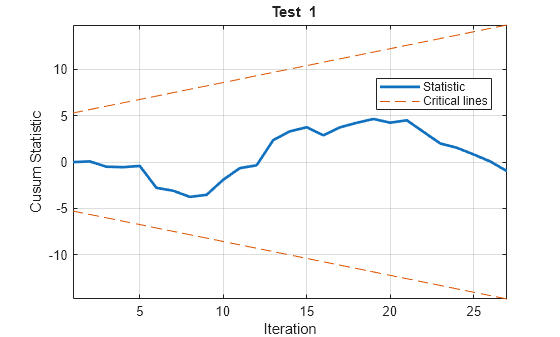
cusumtest(___) plots both the sequence of
cusums and the critical lines resulting from the cusum tests.
cusumtest(
plots on the axes specified by ax,___)ax instead of
the current axes (gca). ax can precede any of the input
argument combinations in the previous syntaxes.
[___,
additionally returns handles to plotted graphics objects. Use elements of
sumPlots]
= cusumtest(___)sumPlots to modify properties of the plot after you
create it.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Limitations
Cusum tests have little power to detect structural changes in the following cases.
Late in the sample period
When multiple changes produce cancellations in the cusums
More About
Tips
The cusum of squares test:
Is a “useful complement to the cusum test, particularly when the departure from constancy of the [recursive coefficients] is haphazard rather than systematic” [1]
Has greater power for cases in which multiple shifts are likely to cancel
Is often suggested for detecting structural breaks in volatility
Alphaspecifies the nominal significance levels for the tests. The actual size of a test depends on various assumptions and approximations thatcusumtestuses to compute the critical lines. Plots of the recursive residuals are the best indicator of structural change. Brown, et al. suggest that the tests “should be regarded as yardsticks for the interpretation of data rather than leading to hard and fast decisions” [1].To produce basic diagnostic plots of the recursive coefficient estimates having the same scale for test
n, enterplot(B(:,:,n)')
recregproduces similar plots, optionally using robust standard error bands.
Algorithms
cusumtesthandles initially constant predictor data using the method suggested in [1]. If a predictor's data is constant for the firstnumCoeffsobservations and this results in multicollinearity with an intercept or another predictor, thencusumtestdrops the predictor from regressions and the computation of recursive residuals until its data changes. Similarly,cusumtesttemporarily holds out terminally constant predictors from backward regressions. Initially constant predictors in backward regressions, or terminally constant predictors in forward regressions, are not held out bycusumtestand can lead to rank deficiency in terminal iterations.cusumtestcomputes critical lines for inference in essentially different ways for the two test statistics. For cusums,cusumtestsolves the normal CDF equation in [1] dynamically for each value ofAlpha. For the cusums of squares test,cusumtestinterpolates parameter values from the table in [2], using the method suggested in [1]. Sample sizes with degrees of freedom less than 4 are below tabulated values, andcusumtestcannot compute critical lines. Sample sizes with degrees of freedom greater than 202 are above tabulated values, andcusumtestuses the critical value associated with the largest tabulated sample size.
References
[1] Brown, R. L., J. Durbin, and J. M. Evans. "Techniques for Testing the Constancy of Regression Relationships Over Time." Journal of the Royal Statistical Society, Series B. Vol. 37, 1975, pp. 149–192.
[2] Durbin, J. "Tests for Serial Correlation in Regression Analysis Based on the Periodogram of Least Squares Residuals." Biometrika. Vol. 56, 1969, pp. 1–15.
Version History
Introduced in R2016aSee Also
recreg | fitlm | LinearModel | chowtest