dtmc
Create discrete-time Markov chain
Description
dtmc creates a discrete-time, finite-state, time-homogeneous Markov chain from a specified state transition matrix.
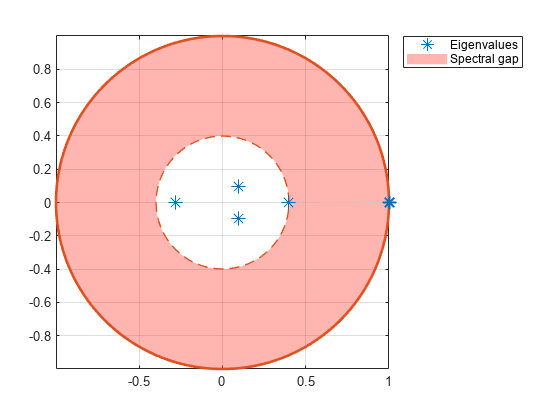
After creating a dtmc object, you can analyze the structure and
evolution of the Markov chain, and visualize the Markov chain in various ways, by using
the object
functions. Also, you can use a dtmc object to specify the
switching mechanism of a Markov-switching dynamic regression model (msVAR).
To create a switching mechanism, governed by threshold transitions and threshold
variable data, for a threshold-switching dynamic regression model, see threshold and
tsVAR.
Creation
Description
mc = dtmc(P)mc specified by the state transition matrix P.
mc = dtmc(P,'StateNames',stateNames)stateNames to the
states.
Input Arguments
Properties
Object Functions
dtmc objects require a fully specified transition matrix P.
Examples
Alternatives
You also can create a Markov chain object using mcmix.
References
[1] Gallager, R.G. Stochastic Processes: Theory for Applications. Cambridge, UK: Cambridge University Press, 2013.
[2] Haggstrom, O. Finite Markov Chains and Algorithmic Applications. Cambridge, UK: Cambridge University Press, 2002.
[3] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[4] Norris, J. R. Markov Chains. Cambridge, UK: Cambridge University Press, 1997.
Version History
Introduced in R2017b