Refine Start Points
About Refining Start Points
If some components of your problem are unconstrained, GlobalSearch and MultiStart use
artificial bounds to generate random start points uniformly in each
component. However, if your problem has far-flung minima, you need
widely dispersed start points to find these minima.
Use these methods to obtain widely dispersed start points:
Give widely separated bounds in your
problemstructure.Use a
RandomStartPointSetobject with theMultiStartalgorithm. Set a large value of theArtificialBoundproperty in theRandomStartPointSetobject.Use a
CustomStartPointSetobject with theMultiStartalgorithm. Use widely dispersed start points.
There are advantages and disadvantages of each method.
| Method | Advantages | Disadvantages |
|---|---|---|
Give bounds in problem | Automatic point generation | Makes a more complex Hessian |
Can use with GlobalSearch | Unclear how large to set the bounds | |
| Easy to do | Changes problem | |
| Bounds can be asymmetric | Only uniform points | |
Large ArtificialBound in RandomStartPointSet | Automatic point generation | MultiStart only |
Does not change problem | Only symmetric, uniform points | |
| Easy to do | Unclear how large to set ArtificialBound | |
CustomStartPointSet | Customizable | MultiStart only |
Does not change problem | Requires programming for generating points |
Methods of Generating Start Points
Uniform Grid
To generate a uniform grid of start points:
Generate multidimensional arrays with
ndgrid. Give the lower bound, spacing, and upper bound for each component.For example, to generate a set of three-dimensional arrays with
First component from –2 through 0, spacing 0.5
Second component from 0 through 2, spacing 0.25
Third component from –10 through 5, spacing 1
[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5);
Place the arrays into a single matrix, with each row representing one start point. For example:
W = [X(:),Y(:),Z(:)];
In this example,
Wis a 720-by-3 matrix.Put the matrix into a
CustomStartPointSetobject. For example:custpts = CustomStartPointSet(W);
Call run
with the CustomStartPointSet object as the
third input. For example,
% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);Perturbed Grid
Integer start points can yield less robust solutions than slightly perturbed start points.
To obtain a perturbed set of start points:
Generate a matrix of start points as in steps 1–2 of Uniform Grid.
Perturb the start points by adding a random normal matrix with 0 mean and relatively small variance.
For the example in Uniform Grid, after making the
Wmatrix, add a perturbation:[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5); W = [X(:),Y(:),Z(:)]; W = W + 0.01*randn(size(W));
Put the matrix into a
CustomStartPointSetobject. For example:custpts = CustomStartPointSet(W);
Call run
with the CustomStartPointSet object as the
third input. For example,
% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);Widely Dispersed Points for Unconstrained Components
Some components of your problem can lack upper or lower bounds. For example:
Although no explicit bounds exist, there are levels that the components cannot attain. For example, if one component represents the weight of a single diamond, there is an implicit upper bound of 1 kg (the Hope Diamond is under 10 g). In such a case, give the implicit bound as an upper bound.
There truly is no upper bound. For example, the size of a computer file in bytes has no effective upper bound. The largest size can be in gigabytes or terabytes today, but in 10 years, who knows?
For truly unbounded components, you can use the following methods of sampling. To generate approximately 1/n points in each region (exp(n),exp(n+1)), use the following formula. If u is random and uniformly distributed from 0 through 1, then r = 2u – 1 is uniformly distributed between –1 and 1. Take
y is symmetric and random. For a variable
bounded below by lb, take
Similarly, for a variable bounded above by ub,
take
For example, suppose you have a three-dimensional problem with
x(1) > 0x(2) < 100x(3) unconstrained
To make 150 start points satisfying these constraints:
u = rand(150,3); r1 = 1./u(:,1); r1 = exp(r1) - exp(1); r2 = 1./u(:,2); r2 = -exp(r2) + exp(1) + 100; r3 = 1./(2*u(:,3)-1); r3 = sign(r3).*(exp(abs(r3)) - exp(1)); custpts = CustomStartPointSet([r1,r2,r3]);
The following is a variant of this algorithm. Generate a number between 0 and infinity by the method for lower bounds. Use this number as the radius of a point. Generate the other components of the point by taking random numbers for each component and multiply by the radius. You can normalize the random numbers, before multiplying by the radius, so their norm is 1. For a worked example of this method, see MultiStart Without Bounds, Widely Dispersed Start Points.
Example: Searching for a Better Solution
MultiStart fails to find the global minimum in
Find Global or Multiple Local Minima. There are two simple ways to search for a better solution:
Use more start points
Give tighter bounds on the search space
Set up the problem structure and MultiStart
object:
problem = createOptimProblem('fminunc',... 'objective',@(x)sawtoothxy(x(1),x(2)),... 'x0',[100,-50],'options',... optimoptions(@fminunc,'Algorithm','quasi-newton')); ms = MultiStart;
Use More Start Points
Run MultiStart on the problem for 200 start
points instead of 50:
rng(14,'twister') % for reproducibility [x,fval,exitflag,output,manymins] = run(ms,problem,200)
MultiStart completed some of the runs from the start points.
53 out of 200 local solver runs converged with a positive local solver exit flag.
x =
1.0e-06 *
-0.2284 -0.5567
fval =
2.1382e-12
exitflag =
2
output =
struct with fields:
funcCount: 32670
localSolverTotal: 200
localSolverSuccess: 53
localSolverIncomplete: 147
localSolverNoSolution: 0
message: 'MultiStart completed some of the runs from the start points.↵↵53 out of 200 local solver runs converged with a positive local solver exit flag.'
manymins =
1x53 GlobalOptimSolution
Properties:
X
Fval
Exitflag
Output
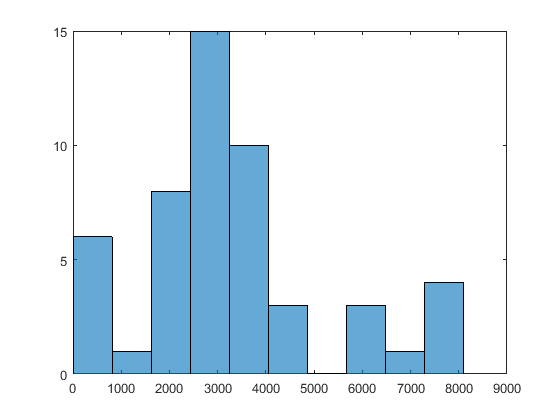
X0This time MultiStart found the global
minimum, and found 51 local minima.
To see the range of local solutions, enter
histogram([manymins.Fval],10).
Tighter Bound on the Start Points
Suppose you believe that the interesting local solutions have absolute values
of all components less than 100. The default value of the bound on start points
is 1000. To use a different value of the bound, generate a RandomStartPointSet with the
ArtificialBound property set to
100:
startpts = RandomStartPointSet('ArtificialBound',100,... 'NumStartPoints',50); [x,fval,exitflag,output,manymins] = run(ms,problem,startpts)
MultiStart completed some of the runs from the start points.
29 out of 50 local solver runs converged with a positive local solver exit flag.
x =
1.0e-08 *
0.9725 -0.6198
fval =
1.4955e-15
exitflag =
2
output =
struct with fields:
funcCount: 7431
localSolverTotal: 50
localSolverSuccess: 29
localSolverIncomplete: 21
localSolverNoSolution: 0
message: 'MultiStart completed some of the runs from the start points.↵↵29 out of 50 local solver runs converged with a positive local solver exit flag.'
manymins =
1x25 GlobalOptimSolution
Properties:
X
Fval
Exitflag
Output
X0MultiStart found the global minimum, and
found 22 distinct local solutions. To see the range of local solutions, enter
histogram([manymins.Fval],10).
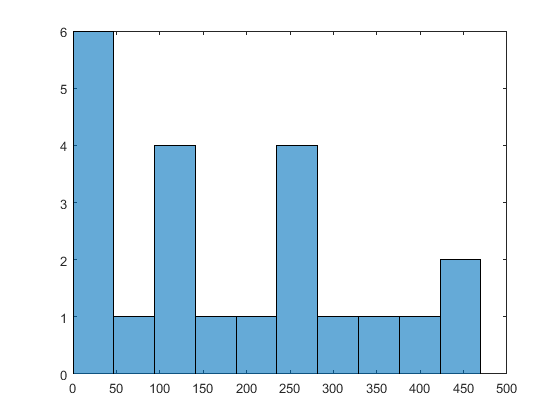
Compared to the minima found in Use More Start Points, this run found better (smaller) minima, and had a higher percentage of successful runs.