What Is the Genetic Algorithm?
The genetic algorithm is a method for solving both constrained and unconstrained optimization problems that is based on natural selection, the process that drives biological evolution. The genetic algorithm repeatedly modifies a population of individual solutions. At each step, the genetic algorithm selects individuals from the current population to be parents and uses them to produce the children for the next generation. Over successive generations, the population "evolves" toward an optimal solution. You can apply the genetic algorithm to solve a variety of optimization problems that are not well suited for standard optimization algorithms, including problems in which the objective function is discontinuous, nondifferentiable, stochastic, or highly nonlinear. The genetic algorithm can address problems of mixed integer programming, where some components are restricted to be integer-valued.
This flow chart outlines the main algorithmic steps. For details, see How the Genetic Algorithm Works.
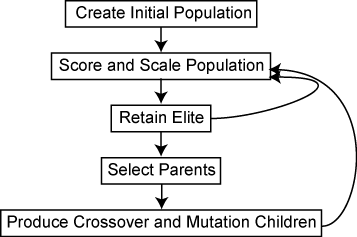
The genetic algorithm uses three main types of rules at each step to create the next generation from the current population:
Selection rules select the individuals, called parents, that contribute to the population at the next generation. The selection is generally stochastic, and can depend on the individuals' scores.
Crossover rules combine two parents to form children for the next generation.
Mutation rules apply random changes to individual parents to form children.

The genetic algorithm differs from a classical, derivative-based, optimization algorithm in two main ways, as summarized in the following table:
| Classical Algorithm | Genetic Algorithm |
|---|---|
Generates a single point at each iteration. The sequence of points approaches an optimal solution. | Generates a population of points at each iteration. The best point in the population approaches an optimal solution. |
Selects the next point in the sequence by a deterministic computation. | Selects the next population by computation which uses random number generators. |
Typically converges quickly to a local solution. | Typically takes many function evaluations to converge. May or may not converge to a local or global minimum. |