noise2meas
Noise component of linear identified model
Description
noiseModel = noise2meas(sys)sys.
Use noise2meas to convert a time-series model (no inputs) to an
input/output model. You can use the converted model for linear analysis, including
viewing pole/zero maps and plotting the step response.
noiseModel = noise2meas(sys,noise)
Examples
Convert a time-series model to an input/output model that may be used by linear analysis tools.
Identify a time-series model.
load iddata9 z9 sys = ar(z9,4,'ls');
sys is an idpoly model with no inputs.
Convert sys to a measured model.
noise_model = noise2meas(sys);
noise_model is an idpoly model with one input.
You can use noise_model for linear analysis functions such as step, iopzmap, etc.
Convert an identified linear model to an input/output model, and normalize its noise variance.
Identify a linear model using data.
load twotankdata;
z = iddata(y,u,0.2);
sys = ssest(z,4);sys is an idss model, with a noise variance of 6.6211e-06. The value of is sqrt(sys.NoiseVariance), which is 0.0026.
View the disturbance matrix.
sys.K
ans = 4×1
0.2719
1.6570
-0.6318
0.2877
Obtain a model that absorbs the noise variance of sys.
noise_model_normalize = noise2meas(sys,'normalize');noise_model_normalize is an idpoly model.
View the matrix for noise_model_normalize.
noise_model_normalize.B
ans = 4×1
0.0007
0.0043
-0.0016
0.0007
As expected, noise_model_normalize.B is equal to L*sys.K.
Compare the bode response with a model that ignores the noise variance of sys.
noise_model_innovation = noise2meas(sys,'innovations'); bodemag(noise_model_normalize,noise_model_innovation); legend('Normalized noise variance','Ignored noise variance');
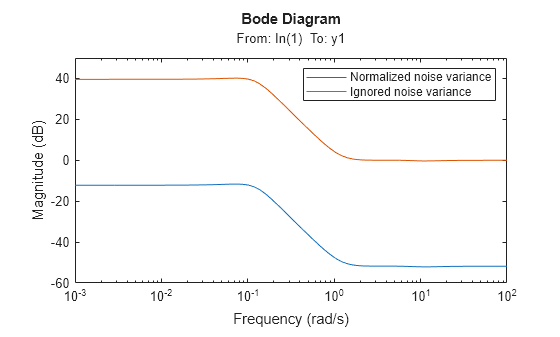
The difference between the bode magnitudes of the noise_model_innovation and noise_model_normalized is approximately 51 dB. As expected, the magnitude difference is approximately equal to 20*log10(L).
Input Arguments
Identified linear model, specified as one of the following model objects.
sys represents the system:
G is the transfer function between the measured input, u(t), and the output, y(t). H is the noise model and describes the effect of the disturbance, e(t), on the model response.
An equivalent state-space representation of sys
is
v(t) is white noise with independent
channels and unit variances. The white-noise signal
e(t) represents the model
innovations and has variance
LLT. The noise-variance
data is stored using the NoiseVariance property of
sys.
Noise variance normalization method, specified as one of the following values.
'innovations'— Noise sources are not normalized and remain as the innovations process.'normalize'— Noise sources are normalized to be independent with unit variance.
Output Arguments
Noise component of identified model, returned as an idss,
idtf, idpoly, or
idfrd object.
The model type of noiseModel depends on the model
type of sys.
noiseModelis anidtfmodel ifsysis anidprocmodel.noiseModelis anidssmodel ifsysis anidgreymodel.noiseModelis the same type of model assysfor all other model types.
To obtain the model coefficients of noiseModel in
state-space form, use ssdata. Similarly, to obtain
the model coefficients in transfer-function form, use tfdata.
Noise Sources Not Normalized
If noise is 'innovations',
then noise2meas returns H and
noiseModel represents the system
An equivalent state-space representation of
noiseModel is
noise2meas returns the noise channels of
sys as the input channels of
noiseModel. The input channels are named using
the format 'e@yk', where yk
corresponds to the OutputName property of an output.
The measured input channels of sys are discarded
and the noise variance is set to zero.
Noise Sources Normalized
If noise is 'normalize', then
noise2meas first normalizes
noiseModel represents the system
or, equivalently, in state-space representation
The input channels are named using the format
'v@yk', where yk corresponds
to the OutputName property of an output.
Version History
Introduced in R2012a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)