Uplink Shared Channel
The physical uplink shared channel is used to transmit the uplink shared channel (UL-SCH) and L1 and L2 control information. The UL-SCH is the transport channel used for transmitting uplink data (a transport block). L1 and L2 control signalling can carry HARQ acknowledgements for received DL-SCH blocks, channel quality reports, and scheduling requests.
UL-SCH Coding
To create the PUSCH payload a transport block of length A, denoted as , undergoes transport block coding. The encoding process includes type-24A CRC calculation, code block segmentation and type-24B CRC attachment if any, turbo encoding, rate matching with RV and code block concatenation. This processing is described in TS 36.212 [1], Sections 5.2.2.1 to 5.2.2.5 and 5.2.2.8.
The transport block coding and control information coding and multiplexing steps are illustrated in the following block diagram.
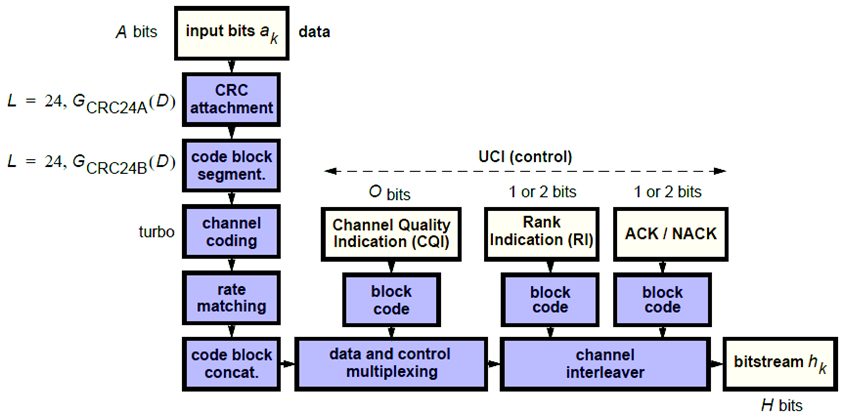
It is possible for the PUSCH to carry only control information and no data. In this case, only the control information coding and multiplexing chain are followed as per the preceding diagram.
Transport Block CRC Attachment
A cyclic redundancy check (CRC) is used for error detection in transport blocks. The entire transport block is used to calculate the CRC parity bits. The transport block is divided by a cyclic generator polynomial, described as in section 5.1.1 of [1], to generate 24 parity bits. These parity bits are then appended to the end of the transport block.
Code Block Segmentation and CRC Attachment
The input block of bits to the code segmentation block is denoted by , where . In LTE, a minimum and maximum code block size is specified, so the block sizes are compatible with the block sizes supported by the turbo interleaver.
The minimum code block size is 40 bits
The maximum code block size, denoted by Z, is 6144 bits
If the length of the input block, B, is greater than the maximum code block size, the input block is segmented.
When the input block is segmented, it is divided into smaller blocks, where L is 24. Therefore, code blocks.
Each code block has a 24-bit CRC attached to the end, calculated as described in Transport Block CRC Attachment, but the generator polynomial, described as in section 5.1.1 of [1] is used.
If required, the algorithm appends filler bits to the start of the segment so that the code block sizes match a set of valid turbo interleaver block sizes. The process is shown in this figure.

If no segmentation is needed, only one code block is produced. If B is less than the minimum size, filler bits (zeros) are added to the beginning of the code block to achieve a total of 40 bits.
Channel Coding
The code blocks undergo turbo coding. Turbo coding is a form of forward error correction that improves the channel capacity by adding redundant information. The turbo encoder scheme used is a Parallel Concatenated Convolutional Code (PCCC) with two recursive convolutional coders and a “contention-free” Quadratic Permutation Polynomial (QPP) interleaver, as shown in this figure.

The output of the encoder is three streams, , , and , to achieve a code rate of 1/3.
Constituent Encoders. The input to the first constituent encoder is the input bit stream to the turbo coding block. The input to the second constituent encoder is the output of the QPP interleaver, a permutation of the input sequence.
Each encoder outputs two sequences, called the systematic sequence and the parity sequence. The systematic sequences are denoted by and the parity sequences are denoted by . Only one of the systematic sequences () is used as an output because the other () is simply a permutation of the chosen systematic sequence. The transfer function for each constituent encoder is given by the following equation.
The first element, 1, represents the systematic output transfer function. The second element, , represents the recursive convolutional output transfer function.
The output for each sequence can be calculated using the transfer function.
The encoder is initialized with all zeros. If the code block
to be encoded is the 0-th and filler bits (F) are
used, the input to the encoder ()
is set to zero and the output ()
and ()
set to <NULL> for .
Trellis Termination for Turbo Encoder. A standard convolutional coder initializes its internal registers to an all zeros state and ensures the coder finishes in an all zeros state by padding the end of the input sequence with k zeros. Since the decoder knows the start and end state of the encoder, it can decode the data. Driving a recursive coder to an all zeros state using this method is not possible. To overcome this problem, trellis termination is used.
Upon termination, the tail bits are fed back to the input of each encoder using a switch. The first three tail bits are used to terminate each encoder.
The QPP Interleaver. The role of the interleaver is to spread the information bits such that in the event of a burst error, the two code streams are affected differently, allowing data to still be recovered.
The output of the interleaver is a permutation of the input data, as shown in these equations.
The variable K is the input length. The variables f1 and f2 are coefficients chosen depending on K, in table 5.1.3-3 of [1]. For example, K=40, f1=3, and f2=10, yields the following sequence.
Rate Matching
The rate matching block creates an output bitstream with a desired code rate. Since the number of bits available for transmission depends on the available resources, the rate matching algorithm is capable of producing any rate. The three bitstreams from the turbo encoder are interleaved, followed by bit collection, to create a circular buffer. Bits are selected and pruned from the buffer to create an output bitstream with the desired code rate. The process is illustrated in this figure.
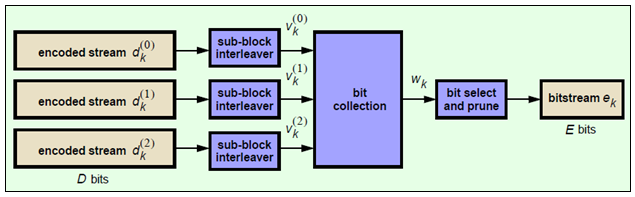
Sub-block Interleaver. The three sub-block interleavers used in the rate matching block are identical. An interleaver permutes the bits it receives. This makes burst errors easier to correct by preventing consecutive corrupt bits.
The sub-block interleaver reshapes the encoded bit sequence, row-by-row, to form a matrix with columns and rows. The variable is determined by finding the minimum integer such that the number of
encoded input bits is . If , ND
<NULL>’s are appended to the front of the encoded sequence. In
this case, .
For blocks and , inter-column permutation is performed on the matrix to reorder the columns as shown in this pattern.
| 0, 16, 8, 24, 4, 20, 12, 28, 2, 18, 10, 26, 6, 22, 14, 30, 1, 17, 9, 25, 5, 21, 13, 29, 3, 19, 11, 27, 7, 23, 15, 31 |
The output of the block interleaver for blocks and is the bit sequence read out column-by-column from the inter-column permuted matrix to create a stream bits long.
For block , the elements of the matrix are permuted separately based on the permutation pattern shown above, but modified to create a permutation which is a function of the variables , , k, and . This process creates three interleaved bitstreams.
Bit Collection, Selection, and Transmission. The bit collection stage creates a virtual circular buffer by combining the three interleaved encoded bit streams.
The sequences and are combined by interlacing successive values from each sequence. This combination is then appended to the end of to create the circular buffer shown in this figure.

Interlacing allows equal levels of protection for each parity sequence.
The algorithm then selects and prunes bits from the circular buffer to create an output sequence length that meets the desired code rate.
The Hybrid Automatic Repeat Request (HARQ) error correction scheme is incorporated into the
rate-matching algorithm of LTE. For any desired code rate the coded bits are output
serially from the circular buffer from a starting location, given by the redundancy
version (RV), wrapping around to the beginning of the buffer if the end of the buffer is
reached. NULL bits are discarded. Different RVs, and hence starting
points, allow for the retransmission of selected data. The ability to select different
starting points enables the following two main methods of recombining data at the
receiver in the HARQ process.
Chase combining — retransmissions contain the same data and parity bit.
Incremental redundancy — retransmissions contain different information, so the receiver gains knowledge on each retransmission.
Code Block Concatenation
At this stage, the rate-matched code blocks are combined again. This is done by sequentially concatenating the blocks to create the output of the channel coding, for .
Channel Coding of Control Information with UL-SCH Data
Control information arrives at the coder in the form of channel quality information (CQI), precoder matrix indication (PMI), rank indication (RI), and HARQ-Indicator (HI). Different control information coding rates are achieved by allocating a different number of coded symbols for transmission. When control information is transmitted on the PUSCH, the channel coding for HI, RI, and CQI is done independently.
The transmission mode determines the bit widths assigned to the various types control information; the corresponding widths for the transmission modes can be found in TS 36.212 [1], Section 5.2.2.6.1-4.
The following sections describe uplink control information on PUSCH with UL-SCH data.
HARQ-ACK Information. The number of coded symbols, Q, used by the UE to transmit the HARQ acknowledgement bits is determined using the number of HARQ bits (1 or 2 depending on the number of codewords present), the scheduled PUSCH bandwidth expressed as a number of subcarriers, the number of SC-FDMA symbols per subframe for the initial PUSCH transmission, and information obtained from the initial PDCCH for the same transport block.
Each positive acknowledgement (ACK) is encoded as a binary 1 and
negative acknowledgement (NACK) is encoded as a binary 0.
If the HARQ-ACK consists of 1-bit of information, ,
corresponding to 1 codeword, then it is first encoded according to
the following table.
| Qm | Encoded HARQ-ACK |
|---|---|
| 2 | |
| 4 | |
| 6 |
In the preceding table, x and y are placeholders used to scramble the HARQ-ACK bits in such a way as to maximize the Euclidean distance of the modulation symbols carrying the HARQ information.
If the HARQ-ACK consists of 2 bits of information, , where and correspond to the first and second codeword, respectively, and , then they are encoded according to the following table.
| Qm | Encoded HARQ-ACK |
|---|---|
| 2 | |
| 4 | |
| 6 |
Rank Indicator. The bit widths, Q, (1 or 2 information bits) for rank indication feedback for PDSCH transmissions are determined using the maximum number of layers according to the corresponding eNodeB antenna configuration and UE category. If RI consists of 1 information bit, , then it is first encoded according to the following table.
| Qm | Encoded RI |
|---|---|
| 2 | |
| 4 | |
| 6 |
In the preceding table, x and y are placeholders used to scramble the HARQ-ACK bits in such a way as to maximize the Euclidean distance of the modulation symbols carrying the HARQ information.
If the RI consists of 2 information bits, , then they are first encoded according to the following table.
| Qm | Encoded RI |
|---|---|
| 2 | |
| 4 | |
| 6 |
Channel Quality Information and Precoder Matrix Indicator. The number of coded symbols, Q, used for channel quality information is determined from the number of CQI bits present, the number of CRC bits, the scheduled PUSCH bandwidth expressed as a number of subcarriers, and information obtained from the PDCCH for the same transport block.
If the payload size is greater than 11 bits, the CQI bit sequence undergoes CRC attachment, convolution channel coding, and rate matching. If the payload size is less than or equal to 11 bits, the channel coding of the CQI is performed using the following steps.
The CQI bits are coded using a (32,O) block code. The codewords of the (32,O) block code use the following equation.
The codewords of the (32,O) block code are a linear combination of the 11 basis sequences denoted in the following table.
i Mi,0 Mi,1 Mi,2 Mi,3 Mi,4 Mi,5 Mi,6 Mi,7 Mi,8 Mi,9 Mi,10 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 1 1 2 1 0 0 1 0 0 1 0 1 1 1 3 1 0 1 1 0 0 0 0 1 0 1 4 1 1 1 1 0 0 0 1 0 0 1 5 1 1 0 0 1 0 1 1 1 0 1 6 1 0 1 0 1 0 1 0 1 1 1 7 1 0 0 1 1 0 0 1 1 0 1 8 1 1 0 1 1 0 0 1 0 1 1 9 1 0 1 1 1 0 1 0 0 1 1 10 1 0 1 0 0 1 1 1 0 1 1 11 1 1 1 0 0 1 1 0 1 0 1 12 1 0 0 1 0 1 0 1 1 1 1 13 1 1 0 1 0 1 0 1 0 1 1 14 1 0 0 0 1 1 0 1 0 0 1 15 1 1 0 0 1 1 1 1 0 1 1 16 1 1 1 0 1 1 1 0 0 1 0 17 1 0 0 1 1 1 0 0 1 0 0 18 1 1 0 1 1 1 1 1 0 0 0 19 1 0 0 0 0 1 1 0 0 0 0 20 1 0 1 0 0 0 1 0 0 0 1 21 1 1 0 1 0 0 0 0 0 1 1 22 1 0 0 0 1 0 0 1 1 0 1 23 1 1 1 0 1 0 0 0 1 1 1 24 1 1 1 1 1 0 1 1 1 1 0 25 1 1 0 0 0 1 1 1 0 0 1 26 1 0 1 1 0 1 0 0 1 1 0 27 1 1 1 1 0 1 0 1 1 1 0 28 1 0 1 0 1 1 1 0 1 0 0 29 1 0 1 1 1 1 1 1 1 0 0 30 1 1 1 1 1 1 1 1 1 1 1 31 1 0 0 0 0 0 0 0 0 0 0
The output sequence is obtained by a circular repetition of the CQI/PMI block, as shown in the following equation.
In the preceding equation, the variable B is 32.
Data and Control Multiplexing
The control and transport data multiplexing is performed such that HARQ-ACK information is present in both slots and is mapped to resources around the demodulation reference signals. The mapping is important, as it assumes the channel estimation around the DRS are of better quality. Thus, the integrity of the HARQ information is maintained.
Channel Interleaver
The channel interleaver implements a time-first mapping of modulation symbols onto the transmit waveform while ensuring that HARQ information is present on both slots and is mapped to resources around the DRS.
Channel Coding of Control Information without UL-SCH Data
When control data is sent on the PUSCH without UL-SCH data the following coding process can be identified: channel coding of control information, mapping and channel interleaving. The fundamental change is the number of bits used to transmit the control information. After determining the bit widths for the various pieces of coded control information, channel coding and rate matching is then performed as per section 1.6 of this document. The coded channel quality information is remapped into columns of symbols before being interleaved with the coded HI and RI.
PUSCH Processing
The Physical Uplink Shared Channel (PUSCH) carries uplink shared channel data and control information. The processing chain for the PUSCH includes scrambling, modulation mapping, precoding, resource element mapping and Single Carrier – Frequency Division Multiple Access (SC-FDMA) modulation. This processing chain is illustrated in the following figure.

Scrambling
The transport codeword is bit-wise multiplied with an orthogonal sequence and a UE-specific scrambling sequence to create the following sequence of symbols for each codeword, q.
The variable is the number of bits transmitted on the PUSCH in one subframe q.
The scrambling sequence is pseudorandom, created using a length-31 Gold sequence generator and initialized using the slot number within the radio network temporary identifier associated with the PUSCH transmission, , the cell ID, , the slot number within the radio frame, , and the codeword index, , at the start of each subframe.
Scrambling with a cell-specific sequence serves the purpose of intercell interference rejection. When a base station descrambles a received bit stream with a known cell specific scrambling sequence, interference from other cells will be descrambled incorrectly and therefore only appear as uncorrelated noise.
Modulation
The scrambled codeword undergoes QPSK, 16QAM, or 64QAM modulation to generate complex valued symbols. This choice provides the flexibility to allow the scheme to maximize the data transmitted depending on the channel conditions.
Precoding
The PUSCH precoding is not the same as the in the downlink (multi-antenna) precoding. The block of complex valued symbols, , is divided into sets. Each set, which has size , corresponds to one SC-FDMA symbol. A Discrete Fourier Transform is then applied to each set, essentially precoding part of the SC-FDMA modulation. The size of the DFT, which is the value of , must have a prime that is a product of 2, 3, or 5, thereby fulfilling the following equation.
In the preceding equation, α2, α3, and α5 are a set of nonnegative integers.
Mapping to Resource Elements
The final stage in the PUSCH processing is to map the symbols to the allocated physical resource elements. The allocation sizes are limited to values whose prime factors are 2, 3 and 5; this limit is imposed by the precoding stage. The symbols are mapped in increasing order beginning with subcarriers, then SC-FDMA symbols. SC-FDMA symbols carrying DRS or SRS are avoided during the mapping process. An example of the order of mapping the output of the precoding stage to the allocated resource blocks is shown in the following figure.

Demodulation Reference Signals (DM-RS) on the PUSCH
Demodulation reference signals associated with the PUSCH are used by the base station to perform channel estimation and allow for coherent demodulation of the received signal.
These reference signals are time-multiplexed with data, whereas in the downlink there is both time and frequency multiplexing. This multiplexing is performed to maintain the single-carrier nature of the SC-FDMA signal, which ensures that all data carriers are contiguous.
DRS Generation
The demodulation reference signals are generated using a base sequence denoted by , which is discussed further in Base Sequence. More specifically, is used to denote the PUSCH DRS sequence and is defined by the following equation.
It is desired that the DRS sequences have small power variations in time and frequency, resulting in high power amplifier efficiency and comparable channel estimation quality for all frequency components. Zadoff-Chu sequences are good candidates, since they exhibit constant power in time and frequency. However, there are a limited number of Zadoff-Chu sequences; therefore, they are not suitable on their own.
The generation and mapping of the DRS associated with the PUSCH are discussed further in the following sections.
Base Sequence. The demodulation reference signals are defined by a cyclic shift, α, of a base sequence, r.
The base sequence, r, is represented in the following equation.
The preceding equation contains the following variables.
, where is the length of the reference signal sequence.
is the base sequence group number.
is the sequence number within the group and only applies to reference signals of length greater than 6 resource blocks.
A phase rotation in the frequency domain (pre-IFFT in the OFDM modulation) is equivalent to a cyclic shift in the time domain (post IFFT in the OFDM modulation). For frequency non-selective channels over the 12 subcarriers of a resource block, it is possible to achieve orthogonality between DRS generated from the same base sequence if for , and assuming the DRS are synchronized in time.
The orthogonality can be exploited to transmit DRS at the same time, using the same frequency resources without mutual interference. Generally, DRS generated from different base sequences will not be orthogonal; however they will present low cross-correlation properties.
To maximize the number of available Zadoff-Chu sequences, a prime length sequence is needed. The minimum sequence length in the UL is 12, the number of subcarriers in a resource block, which is not prime.
Therefore, Zadoff-Chu sequences are not suitable by themselves. There are effectively the following two types of base reference sequences.
those with a sequence length ≥ 36 (spanning 3 or more resource blocks), which use a cyclic extension of Zadoff-Chu sequences
those with a sequence length ≤ 36 (spanning 2 resource blocks), which use a special QPSK sequence
 Base sequences of length ≥ three resource blocks
Base sequences of length ≥ three resource blocks
 Base sequences of length ≤ three resource blocks
Base sequences of length ≤ three resource blocks
DRS Grouping. There are a total of 30 sequence groups, , each containing one sequence for length less than or equal to 60. This corresponds to transmission bandwidths of 1,2,3,4 and 5 resource blocks. Additionally, there are two sequences (one for v = 0 or 1) for length ≥ 72; corresponding to transmission bandwidths of 6 resource blocks or more.
Note that not all values of m are allowed, where m is the number of resource blocks used for transmission. Only values for m that are the product of powers of 2, 3 and 5 are valid, as shown in the following equation.
The reason for this restriction is that the DFT sizes of the SC-FDMA precoding operation are limited to values which are the product of powers of 2, 3 and 5. The DFT operation can span more than one resource block, and since each resource block has 12 subcarriers, the total number of subcarriers fed to the DFT will be 12m. Since the result of 12m has to be the product of powers of 2, 3 and 5 this implies that the number of resource blocks must themselves be the product of powers of 2, 3 and 5. Therefore values of m such as 7, 11, 14, 19, etc. are not valid.
For a given time slot, the uplink reference signal sequences to use within a cell are taken from one specific sequence group. If the same group is to be used for all slots then this is known as fixed assignment. On the other hand, if the group number u varies for all slots within a cell this is known as group hopping.
DRS Resource Mapping
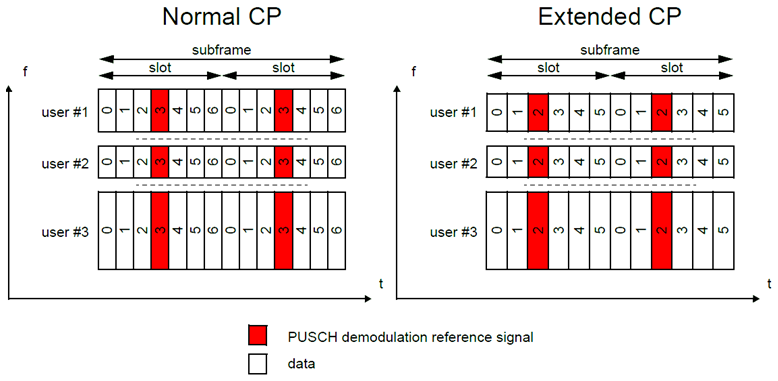
The PUSCH demodulation reference signal is mapped to the 4th SC-FDMA symbol of the slot during normal cyclic prefix and to every 3rd SC-FDMA slot during extended cyclic prefix. This resource mapping is shown in the following figure.
References
[1] 3GPP TS 36.212. “Evolved Universal Terrestrial Radio Access (E-UTRA); Multiplexing and channel coding.” 3rd Generation Partnership Project; Technical Specification Group Radio Access Network. URL: https://www.3gpp.org.
See Also
lteULSCH | lteULSCHInfo | ltePUSCH | ltePUSCHIndices | ltePUSCHDRS | ltePUSCHDRSIndices | lteULResourceGrid