interp2
Interpolation for 2-D gridded data in meshgrid format
Syntax
Description
Vq = interp2(X,Y,V,Xq,Yq)X and Y contain
the coordinates of the sample points. V contains
the corresponding function values at each sample point. Xq and Yq contain
the coordinates of the query points.
Vq = interp2(___,method,extrapval)extrapval, a scalar value that is assigned
to all queries that lie outside the domain of the sample points.
If you omit the extrapval argument for queries
outside the domain of the sample points, then based on the method argument interp2 returns
one of the following:
Extrapolated values for the
'spline'and'makima'methodsNaNvalues for other interpolation methods
Examples
Coarsely sample the peaks function.
[X,Y] = meshgrid(-3:3); V = peaks(X,Y);
Plot the coarse sampling.
figure
surf(X,Y,V)
title('Original Sampling');
Create the query grid with spacing of 0.25.
[Xq,Yq] = meshgrid(-3:0.25:3);
Interpolate at the query points.
Vq = interp2(X,Y,V,Xq,Yq);
Plot the result.
figure
surf(Xq,Yq,Vq);
title('Linear Interpolation Using Finer Grid');
Coarsely sample the peaks function.
[X,Y] = meshgrid(-3:3); V = peaks(7);
Plot the coarse sampling.
figure
surf(X,Y,V)
title('Original Sampling');
Create the query grid with spacing of 0.25.
[Xq,Yq] = meshgrid(-3:0.25:3);
Interpolate at the query points, and specify cubic interpolation.
Vq = interp2(X,Y,V,Xq,Yq,'cubic');Plot the result.
figure
surf(Xq,Yq,Vq);
title('Cubic Interpolation Over Finer Grid');
Load some image data into the workspace.
load flujet.mat colormap gray
Isolate a small region of the image and cast it to single-precision.
V = single(X(200:300,1:25));
Display the image region.
imagesc(V); axis off title('Original Image')

Insert interpolated values by repeatedly dividing the intervals between points of the refined grid five times in each dimension.
Vq = interp2(V,5);
Display the result.
imagesc(Vq); axis off title('Linear Interpolation')

Coarsely sample a function over the range, [-2, 2] in both dimensions.
[X,Y] = meshgrid(-2:0.75:2); R = sqrt(X.^2 + Y.^2)+ eps; V = sin(R)./(R);
Plot the coarse sampling.
figure
surf(X,Y,V)
xlim([-4 4])
ylim([-4 4])
title('Original Sampling')
Create the query grid that extends beyond the domain of X and Y.
[Xq,Yq] = meshgrid(-3:0.2:3);
Perform cubic interpolation within the domain of X and Y, and assign all queries that fall outside to zero.
Vq = interp2(X,Y,V,Xq,Yq,'cubic',0);Plot the result.
figure
surf(Xq,Yq,Vq)
title('Cubic Interpolation with Vq=0 Outside Domain of X and Y');
Input Arguments
Sample grid points, specified as real matrices or vectors. The sample grid points must be unique.
If
XandYare matrices, then they contain the coordinates of a full grid (in meshgrid format). Use themeshgridfunction to create theXandYmatrices together. Both matrices must be the same size.If
XandYare vectors, then they are treated as grid vectors. The values in both vectors must be strictly monotonic, either increasing or decreasing.
Example: [X,Y] = meshgrid(1:30,-10:10)
Data Types: single | double
Sample values, specified as a real or complex matrix. The size
requirements for V depend on the size of X and Y:
If
XandYare matrices representing a full grid (inmeshgridformat), thenVmust be the same size asXandY.If
XandYare grid vectors, thenVmust be a matrix containinglength(Y)rows andlength(X)columns.
If V contains complex numbers, then interp2 interpolates
the real and imaginary parts separately.
Example: rand(10,10)
Data Types: single | double
Complex Number Support: Yes
Query points, specified as a real scalars, vectors, matrices, or arrays.
If
XqandYqare scalars, then they are the coordinates of a single query point.If
XqandYqare vectors of different orientations, thenXqandYqare treated as grid vectors.If
XqandYqare vectors of the same size and orientation, thenXqandYqare treated as scattered points in 2-D space.If
XqandYqare matrices, then they represent either a full grid of query points (inmeshgridformat) or scattered points.If
XqandYqare N-D arrays, then they represent scattered points in 2-D space.
Example: [Xq,Yq] = meshgrid((1:0.1:10),(-5:0.1:0))
Data Types: single | double
Refinement factor, specified as a real, nonnegative, integer
scalar. This value specifies the number of times to repeatedly divide
the intervals of the refined grid in each dimension. This results
in 2^k-1 interpolated points between sample values.
If k is 0, then Vq is
the same as V.
interp2(V,1) is the same as interp2(V).
The following illustration shows the placement of interpolated
values (in red) among nine sample values (in black) for k=2.

Example: interp2(V,2)
Data Types: single | double
Interpolation method, specified as one of the options in this table.
| Method | Description | Continuity | Comments |
|---|---|---|---|
'linear' | The interpolated value at a query point is based on linear interpolation of the values at neighboring grid points in each respective dimension. This is the default interpolation method. | C0 |
|
'nearest' | The interpolated value at a query point is the value at the nearest sample grid point. | Discontinuous |
|
'cubic' | The interpolated value at a query point is based on a cubic interpolation of the values at neighboring grid points in each respective dimension. The interpolation is based on a cubic convolution. | C1 |
|
'makima' | Modified Akima cubic Hermite interpolation. The interpolated value at a query point is based on a piecewise function of polynomials with degree at most three evaluated using the values of neighboring grid points in each respective dimension. The Akima formula is modified to avoid overshoots. | C1 |
|
'spline' | The interpolated value at a query point is based on a cubic interpolation of the values at neighboring grid points in each respective dimension. The interpolation is based on a cubic spline using not-a-knot end conditions. | C2 |
|
Function value outside domain of X and Y,
specified as a real or complex scalar. interp2 returns
this constant value for all points outside the domain of X and Y.
Example: 5
Example: 5+1i
Data Types: single | double
Complex Number Support: Yes
Output Arguments
Interpolated values, returned as a real or complex scalar, vector,
or matrix. The size and shape of Vq depends on
the syntax you use and, in some cases, the size and value of the input
arguments.
| Syntaxes | Special Conditions | Size of Vq | Example |
|---|---|---|---|
interp2(X,Y,V,Xq,Yq)interp2(V,Xq,Yq)and variations of these syntaxes that include method or extrapval | Xq, Yq are scalars | Scalar | size(Vq) = [1 1] when you pass Xq and Yq as
scalars. |
| Same as above | Xq, Yq are vectors of
the same size and orientation | Vector of same size and orientation as Xq and Yq | If size(Xq) = [100 1]and size(Yq)
= [100 1], then size(Vq) = [100
1]. |
| Same as above | Xq, Yq are vectors of
mixed orientation | Matrix in which the number of rows is length(Yq),
and the number of columns is length(Xq) | If size(Xq) = [1 100]and size(Yq)
= [50 1], then size(Vq) = [50 100]. |
| Same as above | Xq, Yq are matrices or
arrays of the same size | Matrix or array of the same size as Xq and Yq | If size(Xq) = [50 25]and size(Yq)
= [50 25], then size(Vq) = [50
25]. |
interp2(V,k)and variations of this syntax that include method or extrapval | None | Matrix in which the number of rows is: | If size(V) = [10 20]and k
= 2, then size(Vq) = [37 77]. |
More About
A set of values that are always increasing
or decreasing, without reversals. For example, the sequence, a
= [2 4 6 8] is strictly monotonic and increasing. The sequence, b
= [2 4 4 6 8] is not strictly monotonic because there is
no change in value between b(2) and b(3).
The sequence, c = [2 4 6 8 6] contains a reversal
between c(4) and c(5), so it
is not monotonic at all.
For interp2, the full
grid is a pair of matrices whose elements represent a grid of points
over a rectangular region. One matrix contains the x-coordinates,
and the other matrix contains the y-coordinates.
The values in the x-matrix are strictly monotonic and increasing
along the rows. The values along its columns are constant. The values
in the y-matrix are strictly monotonic and increasing
along the columns. The values along its rows are constant. Use the meshgrid function to create a full grid
that you can pass to interp2.
For example, the following code creates a full grid for the region, –1 ≤ x ≤ 3 and 1 ≤ y ≤ 4:
[X,Y] = meshgrid(-1:3,(1:4))
X =
-1 0 1 2 3
-1 0 1 2 3
-1 0 1 2 3
-1 0 1 2 3
Y =
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4Grid vectors are a more compact format to represent a grid than the full grid. The
relation between the two formats and the matrix of sample values
V is
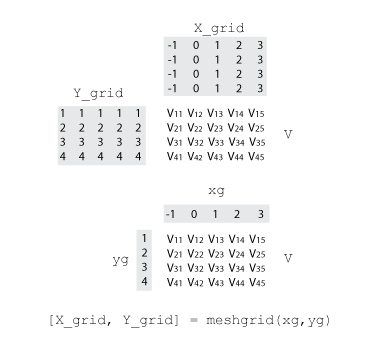
For interp2, grid vectors consist of a pair of vectors
that define the x- and y-coordinates in a
grid. The row vector defines x-coordinates, and the column vector
defines y-coordinates.

For example, the following code creates the grid vectors that specify the region, –1 ≤ x ≤ 3 and 1 ≤ y ≤ 4:
x = -1:3; y = (1:4)';
For interp2, scattered
points consist of a pair of arrays that define a collection of points
scattered in 2-D space. One array contains the x-coordinates,
and the other contains the y-coordinates.
For example, the following code specifies the points, (2,7), (5,3), (4,1), and (10,9):
x = [2 5; 4 10]; y = [7 3; 1 9];
Extended Capabilities
Usage notes and limitations:
XqandYqmust be the same size. Usemeshgridto evaluate on a grid.For best results, provide
XandYas vectors. The values in these vectors must be strictly monotonic and increasing.Code generation does not support the
'makima'interpolation method.For the
'cubic'interpolation method, if the grid does not have uniform spacing, an error results. In this case, use the'spline'interpolation method.For best results when you use the
'spline'interpolation method:Use
meshgridto create the inputsXqandYq.Use a small number of interpolation points relative to the dimensions of
V. Interpolating over a large set of scattered points can be inefficient.
Usage notes and limitations:
XqandYqmust be the same size. Usemeshgridto evaluate on a grid.For best results, provide
XandYas vectors. The values in these vectors must be strictly monotonic and increasing.Code generation does not support the
'makima'interpolation method.For the
'cubic'interpolation method, if the grid does not have uniform spacing, an error results. In this case, use the'spline'interpolation method.For best results when you use the
'spline'interpolation method:Use
meshgridto create the inputsXqandYq.Use a small number of interpolation points relative to the dimensions of
V. Interpolating over a large set of scattered points can be inefficient.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The interp2 function
supports GPU array input with these usage notes and limitations:
Vmust be a double or single 2-D array.Vcan be real or complex.Vcannot be a vector.XandYmust:Have the same type (double or single).
Be finite vectors or 2-D arrays with increasing and nonrepeating elements in corresponding dimensions.
Align with Cartesian axes when
XandYare nonvector 2-D arrays (as if they were produced bymeshgrid).Have dimensions consistent with
V.
XqandYqmust be vectors or arrays of the same type (double or single). IfXqandYqare arrays, then they must have the same size. If they are vectors with different lengths, then they must have different orientations.methodmust be'linear','nearest', or'cubic'.The extrapolation for the out-of-boundary input is not supported.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
See Also
griddata | interp1 | interp3 | interpn | meshgrid | griddedInterpolant | scatteredInterpolant
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)