lsqr
Solve system of linear equations — least-squares method
Syntax
Description
x = lsqr(A,b)A*x = b for
x using the Least Squares Method.
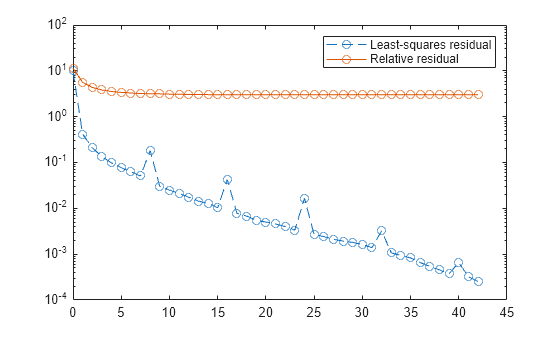
lsqr finds a least squares solution for x that
minimizes norm(b-A*x). When A is consistent, the least
squares solution is also a solution of the linear system. When the attempt is successful,
lsqr displays a message to confirm convergence. If
lsqr fails to converge after the maximum number of iterations or
halts for any reason, it displays a diagnostic message that includes the relative residual
norm(b-A*x)/norm(b) and the iteration number at which the method
stopped.
[
returns a flag that specifies whether the algorithm successfully converged. When
x,flag] = lsqr(___)flag = 0, convergence was successful. You can use this output syntax
with any of the previous input argument combinations. When you specify the
flag output, lsqr does not display any diagnostic
messages.
Examples
Input Arguments
Output Arguments
More About
Tips
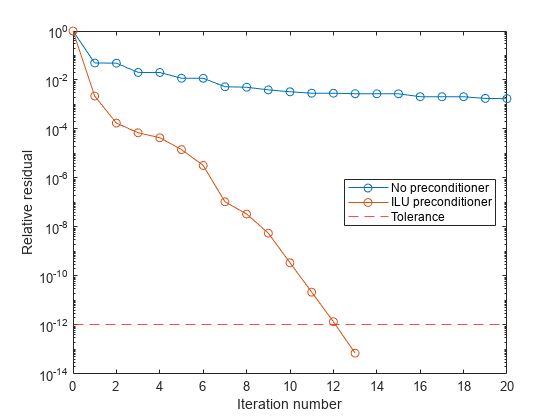
Convergence of most iterative methods depends on the condition number of the coefficient matrix,
cond(A). WhenAis square, you can useequilibrateto improve its condition number, and on its own this makes it easier for most iterative solvers to converge. However, usingequilibratealso leads to better quality preconditioner matrices when you subsequently factor the equilibrated matrixB = R*P*A*C.You can use matrix reordering functions such as
dissectandsymrcmto permute the rows and columns of the coefficient matrix and minimize the number of nonzeros when the coefficient matrix is factored to generate a preconditioner. This can reduce the memory and time required to subsequently solve the preconditioned linear system.
References
[1] Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.
[2] Paige, C. C. and M. A. Saunders, "LSQR: An Algorithm for Sparse Linear Equations And Sparse Least Squares," ACM Trans. Math. Soft., Vol.8, 1982, pp. 43-71.