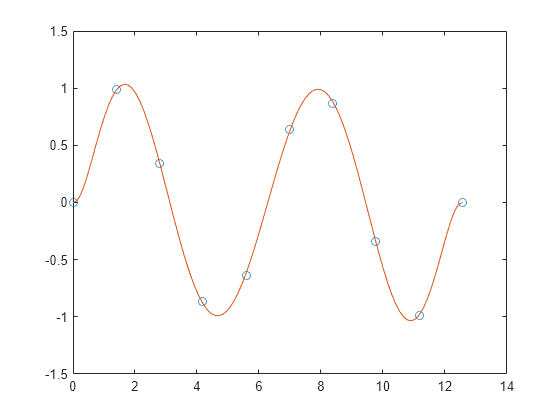
polyfit
Polynomial curve fitting
Description
[
performs centering and scaling to improve the numerical properties of both the
polynomial and the fitting algorithm. This syntax additionally returns
p,S,mu]
= polyfit(x,y,n)mu, which is a two-element vector with centering and scaling
values. mu(1) is mean(x), and
mu(2) is std(x). Using these values,
polyfit centers x at zero and scales it to
have unit standard deviation,
Examples
Input Arguments
Output Arguments
Limitations
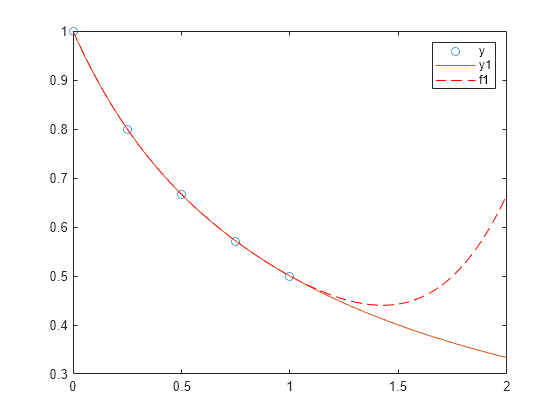
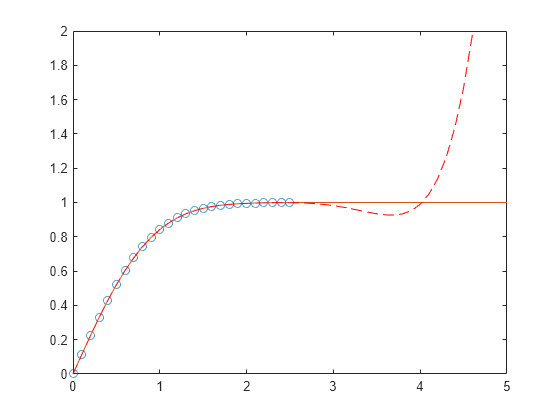
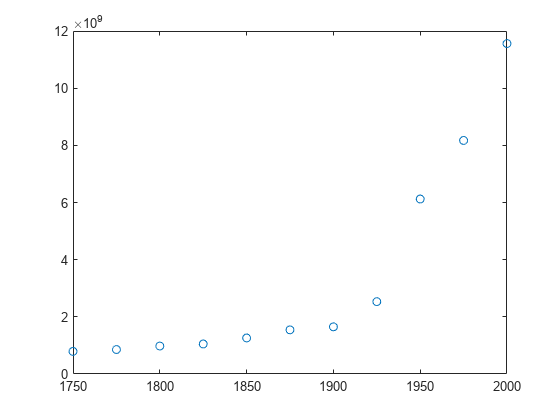
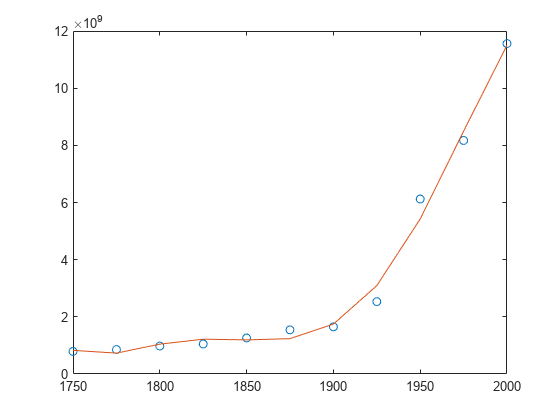
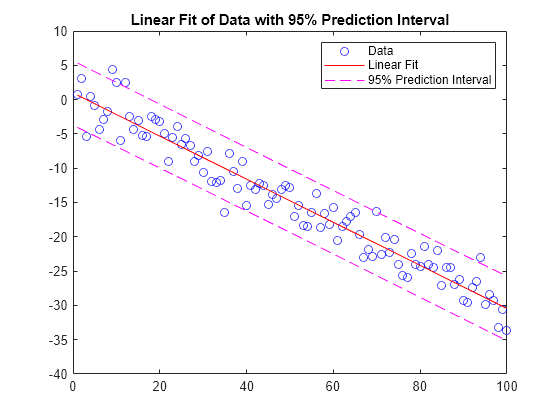
In problems with many points, increasing the degree of the polynomial fit using
polyfitdoes not always result in a better fit. High-order polynomials can be oscillatory between the data points, leading to a poorer fit to the data. In those cases, you might use a low-order polynomial fit (which tends to be smoother between points) or a different technique, depending on the problem.Polynomials are unbounded, oscillatory functions by nature. Therefore, they are not well-suited to extrapolating bounded data or monotonic (increasing or decreasing) data.
Algorithms
polyfit uses x to form
Vandermonde matrix V with n+1 columns
and m = length(x) rows, resulting in the linear
system
which polyfit solves with p = V\y.
Since the columns in the Vandermonde matrix are powers of the vector x,
the condition number of V is often large for high-order
fits, resulting in a singular coefficient matrix. In those cases centering
and scaling can improve the numerical properties of the system to
produce a more reliable fit.