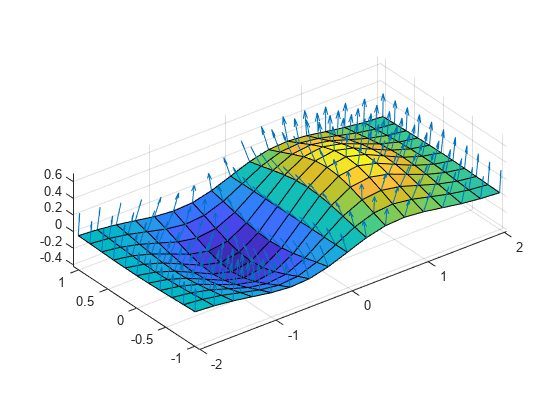
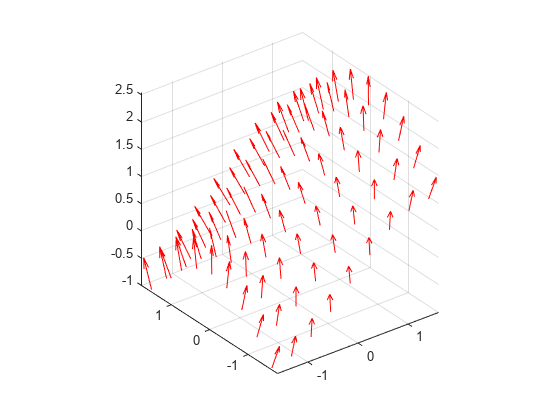
quiver3
3-D quiver or vector plot
Syntax
Description
quiver3(
plots arrows with directional components X,Y,Z,U,V,W)U, V,
and W at the Cartesian coordinates specified by
X, Y, and Z. For example,
the first arrow originates from the point X(1),
Y(1), and Z(1), extends in the direction of the
x-axis according to U(1), extends in the direction
of the y-axis according to V(1), and extends in the
direction of the z-axis according to W(1). By
default, the quiver3 function scales the arrow lengths so that they
do not overlap.
quiver3(
plots arrows with directional components specified by Z,U,V,W)U,
V, and W at equally spaced points along the
surface Z.
If
Zis a vector, then the x-coordinates of the arrows range from 1 to the number of elements inZand the y-coordinates are all 1.If
Zis a matrix, then the x-coordinates of the arrows range from 1 to the number of columns inZand the y-coordinates range from 1 to the number of rows inZ.
quiver3(___, adjusts the
length of arrows:scale)
When
scaleis a positive number, thequiver3function automatically adjusts the lengths of arrows so they do not overlap, then stretches them by a factor ofscale. For example, ascaleof 2 doubles the length of arrows, and ascaleof 0.5 halves the length of arrows.When
scaleis'off'or0, such asquiver3(X,Y,Z,U,V,W,'off'), then automatic scaling is disabled.
quiver3(___,
fills the markers specified by LineSpec,'filled')LineSpec.
quiver3(___,
specifies quiver properties using one or more name-value pair arguments. For a list of
properties, see Quiver Properties. Specify name-value pair
arguments after all other input arguments. Name-value pair arguments apply to all of the
arrows in the quiver plot.Name,Value)
q = quiver3(___) returns a Quiver
object. This object is useful for controlling the properties of the quiver plot after
creating it.
Examples
Input Arguments
Name-Value Arguments
Tips
To create a 3-D quiver plot using cylindrical or spherical coordinates, first convert them
to Cartesian coordinates using the pol2cart or sph2cart function.
Extended Capabilities
Version History
Introduced before R2006a