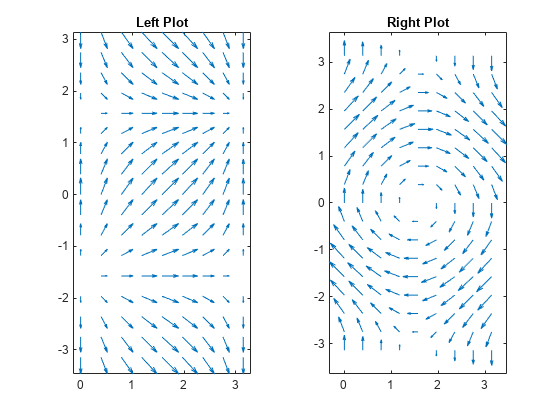
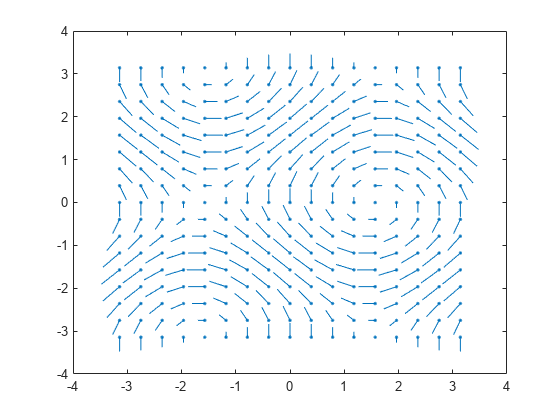
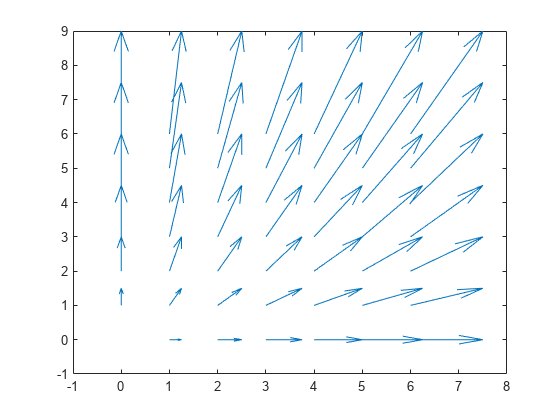quiver
Quiver or vector plot
Syntax
Description
quiver(
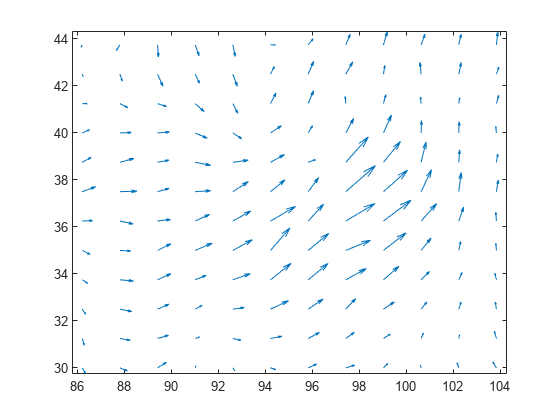
plots arrows with directional components X,Y,U,V)U and V
at the Cartesian coordinates specified by X and
Y. For example, the first arrow originates from the point
X(1) and Y(1), extends horizontally according to
U(1), and extends vertically according to V(1). By
default, the quiver function scales the arrow lengths so that they do
not overlap.
quiver( plots
arrows with directional components specified by U,V)U and
V at equally spaced points.
If
UandVare vectors, then the x-coordinates of the arrows range from 1 to the number of elements inUandV, and the y-coordinates are all 1.If
UandVare matrices, then the x-coordinates of the arrows range from 1 to the number of columns inUandV, and the y-coordinates of the arrows range from 1 to the number of rows inUandV.
quiver(___, adjusts the
length of arrows:scale)
When
scaleis a positive number, thequiverfunction automatically adjusts the lengths of arrows so they do not overlap, then stretches them by a factor ofscale. For example, ascaleof 2 doubles the length of arrows, and ascaleof 0.5 halves the length of arrows.When
scaleis'off'or0, such asquiver(X,Y,U,V,'off'), then automatic scaling is disabled.
quiver(___,
fills the markers specified by LineSpec,'filled')LineSpec.
quiver(___, specifies
quiver properties using one or more name-value pair arguments. For a list of properties,
see Quiver Properties. Specify name-value pair
arguments after all other input arguments. Name-value pair arguments apply to all of the
arrows in the quiver plot.Name,Value)
q = quiver(___) returns a Quiver
object. This object is useful for controlling the properties of the quiver plot after
creating it.
Examples
Input Arguments
Name-Value Arguments
Tips
To create a quiver plot using polar coordinates, first convert them to Cartesian
coordinates using the pol2cart function.
Extended Capabilities
Version History
Introduced before R2006a