uniquetol
Unique values within tolerance
Syntax
Description
C = uniquetol(A,tol)A using tolerance tol.
Two values, u and v, are within
tolerance if
abs(u-v) <= tol*max(abs(A(:)))
That is, uniquetol scales the tol input
based on the magnitude of the data.
uniquetol is similar to unique.
Whereas unique performs exact comparisons, uniquetol performs
comparisons using a tolerance.
C = uniquetol(A,tol,occurrence)occurrence is 'highest', specifies
that when several values are within tolerance of each other, the highest value
should be selected as being unique. The default for
occurrence is 'lowest', which selects
the lowest value as being unique.
[___] = uniquetol(___, uses
additional options specified by one or more Name-Value pair arguments
using any of the input or output argument combinations in previous
syntaxes. For example, Name,Value)uniquetol(A,'ByRows',true) determines
the unique rows in A.
Examples
Create a vector x. Obtain a second vector y by transforming and untransforming x. This transformation introduces round-off differences in y.
x = (1:6)'*pi; y = 10.^log10(x);
Verify that x and y are not identical by taking the difference.
x-y
ans = 6×1
10-14 ×
0.0444
0
0
0
0
-0.3553
Use unique to find the unique elements in the concatenated vector [x;y]. The unique function performs exact comparisons and determines that some values in x are not exactly equal to values in y. These are the same elements that have a nonzero difference in x-y. Thus, c contains values that appear to be duplicates.
c = unique([x;y])
c = 8×1
3.1416
3.1416
6.2832
9.4248
12.5664
15.7080
18.8496
18.8496
Use uniquetol to perform the comparison using a small tolerance. uniquetol treats elements that are within tolerance as equal.
C = uniquetol([x;y])
C = 6×1
3.1416
6.2832
9.4248
12.5664
15.7080
18.8496
By default, uniquetol looks for unique elements that are within tolerance, but it also can find unique rows of a matrix that are within tolerance.
Create a numeric matrix, A. Obtain a second matrix, B, by transforming and untransforming A. This transformation introduces round-off differences to B.
A = [0.05 0.11 0.18; 0.18 0.21 0.29; 0.34 0.36 0.41; 0.46 0.52 0.76]; B = log10(10.^A);
Use unique to find the unique rows in A and B. The unique function performs exact comparisons and determines that all of the rows in the concatenated matrix [A;B] are unique, even though some of the rows differ by only a small amount.
unique([A;B],'rows')ans = 8×3
0.0500 0.1100 0.1800
0.0500 0.1100 0.1800
0.1800 0.2100 0.2900
0.1800 0.2100 0.2900
0.3400 0.3600 0.4100
0.3400 0.3600 0.4100
0.4600 0.5200 0.7600
0.4600 0.5200 0.7600
Use uniquetol to find the unique rows. uniquetol treats rows that are within tolerance as equal.
uniquetol([A;B],'ByRows',true)ans = 4×3
0.0500 0.1100 0.1800
0.1800 0.2100 0.2900
0.3400 0.3600 0.4100
0.4600 0.5200 0.7600
Create a vector, x. Obtain a second vector, y, by transforming and untransforming x. This transformation introduces round-off differences to some elements in y.
x = (1:5)'*pi; y = 10.^log10(x);
Combine x and y into a single vector, A. Use uniquetol to reconstruct A, treating the values that are within tolerance as equal.
A = [x;y]
A = 10×1
3.1416
6.2832
9.4248
12.5664
15.7080
3.1416
6.2832
9.4248
12.5664
15.7080
[C,IA,IC] = uniquetol(A); newA = C(IC)
newA = 10×1
3.1416
6.2832
9.4248
12.5664
15.7080
3.1416
6.2832
9.4248
12.5664
15.7080
You can use newA with == or functions that use exact equality like isequal or unique in subsequent code.
D1 = unique(A)
D1 = 6×1
3.1416
3.1416
6.2832
9.4248
12.5664
15.7080
D2 = unique(newA)
D2 = 5×1
3.1416
6.2832
9.4248
12.5664
15.7080
Use the occurrence option to control which elements uniquetol selects as being unique.
Create a vector and find which elements are unique within a tolerance of 1e-1.
a = [1 1.1 1.11 1.12 1.13 2]; c = uniquetol(a,1e-1)
c = 1×2
1 2
Since the first five elements in A all have similar values with respect to the tolerance of 1e-1, only the lowest value among them is selected as being unique. This is because uniquetol begins with the lowest value in a and does not find a new element that is not within tolerance until the 2 at the end of the vector.
Use the 'highest' option to specify that uniquetol should begin with the highest value in a. Now, the 1.13 element is selected as being unique since uniquetol works down from the highest values.
d = uniquetol(a,1e-1,'highest')d = 1×2
1.1300 2.0000
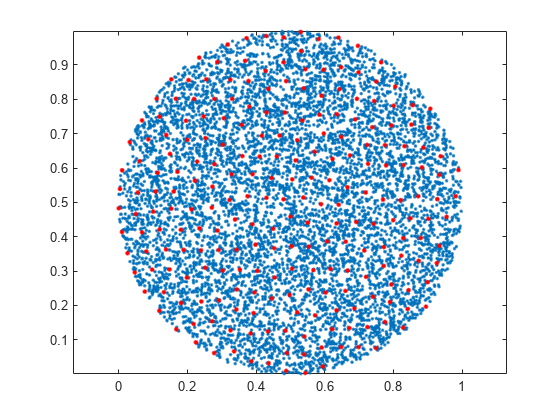
Create a cloud of 2-D sample points constrained to be inside a circle of radius 0.5 centered at the point .
x = rand(10000,2); insideCircle = sqrt((x(:,1)-.5).^2+(x(:,2)-.5).^2)<0.5; y = x(insideCircle,:);
Find a reduced set of points, such that each point of the original dataset is within tolerance of a point.
tol = 0.05;
C = uniquetol(y,tol,'ByRows',true);Plot the reduced set of points as red dots on top of the original data set. The red dots are all members of the original data set. All the red dots are at least a distance tol apart.
plot(y(:,1),y(:,2),'.') hold on axis equal plot(C(:,1), C(:,2), '.r', 'MarkerSize', 10)
Create a vector of random numbers and determine the unique elements using a tolerance. Specify OutputAllIndices as true to return all of the indices for the elements that are within tolerance of the unique values.
A = rand(100,1);
[C,IA] = uniquetol(A,1e-2,'OutputAllIndices',true);Find the average value of the elements that are within tolerance of the value C(2).
C(2)
ans = 0.0318
allA = A(IA{2})allA = 3×1
0.0357
0.0318
0.0344
aveA = mean(allA)
aveA = 0.0340
By default, uniquetol uses a tolerance test of the form abs(u-v) <= tol*DS, where DS automatically scales based on the magnitude of the input data. You can specify a different DS value to use with the DataScale option. However, absolute tolerances (where DS is a scalar) do not scale based on the magnitude of the input data.
First, compare two small values that are a distance eps apart. Specify tol and DS to make the within tolerance equation: abs(u-v) <= 10^-6.
x = 0.1;
uniquetol([x, exp(log(x))], 10^-6, 'DataScale', 1)ans = 0.1000
Next, increase the magnitude of the values. The round-off error in the calculation exp(log(x)) is proportional to the magnitude of the values, specifically to eps(x). Even though the two large values are a distance eps from one another, eps(x) is now much larger. Therefore, 10^-6 is no longer a suitable tolerance.
x = 10^10;
uniquetol([x, exp(log(x))], 10^-6, 'DataScale', 1)ans = 1×2
1010 ×
1.0000 1.0000
Correct this issue by using the default (scaled) value of DS.
format long
Y = [0.1 10^10];
uniquetol([Y, exp(log(Y))])ans = 1×2
1010 ×
0.000000000010000 1.000000000000000
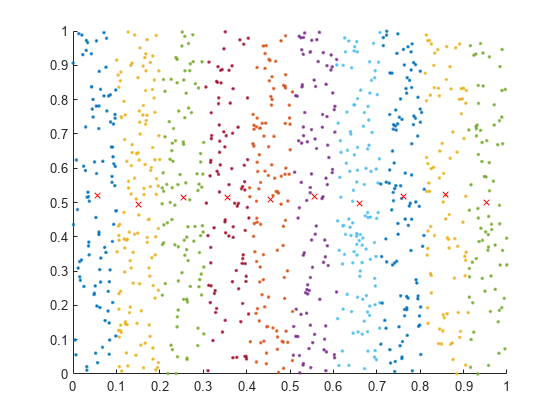
Create a set of random 2-D points, then use uniquetol to group the points into vertical bands that have a similar (within tolerance) x-coordinate. Use these options with uniquetol:
Specify
ByRowsastruesince the point coordinates are in the rows ofA.Specify
OutputAllIndicesastrueto return the indices for all points that have an x-coordinate within tolerance of each other.Specify
DataScaleas[1 Inf]to use an absolute tolerance for thex-coordinate while ignoring they-coordinate.
A = rand(1000,2); DS = [1 Inf]; [C,IA] = uniquetol(A, 0.1, 'ByRows', true, ... 'OutputAllIndices', true, 'DataScale', DS);
Plot the points and average value for each band.
hold on for k = 1:length(IA) plot(A(IA{k},1), A(IA{k},2), '.') meanAi = mean(A(IA{k},:)); plot(meanAi(1), meanAi(2), 'xr') end
Input Arguments
Query array, specified as a scalar, vector, matrix, or multidimensional
array. A must be real and full.
Data Types: single | double
Comparison tolerance, specified as a positive, real scalar.
uniquetol scales the tol input
using the maximum absolute value in input array A. Then
uniquetol uses the resulting scaled comparison
tolerance to determine which elements in A are unique. If
two elements in A are within tolerance of each other,
then uniquetol considers them to be equal.
Two values, u and v, are within
tolerance if abs(u-v) <= tol*max(abs(A)).
To specify an absolute tolerance, specify both tol and
the 'DataScale' Name-Value pair.
Example: tol = 0.05
Example: tol = 1e-8
Example: tol = eps
Data Types: single | double
Occurrence of unique values, specified as one of the options in this
table. The value of occurrence determines which elements
uniquetol selects as being unique.
| Option | Description |
|---|---|
'lowest' |
|
'highest' |
|
Example: C = uniquetol(A,tol,'highest')
Example: C = uniquetol([1 2 3],2,'highest') returns
3, since uniquetol starts with
the highest value in the input and all other values are within
tolerance.
Data Types: char | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: C = uniquetol(A,'ByRows',true)
Output index type, specified as the comma-separated pair consisting
of 'OutputAllIndices' and either false (default), true, 0,
or 1. uniquetol interprets
numeric 0 as false and numeric 1 as true.
When OutputAllIndices is true,
the uniquetol function returns the second output, IA,
as a cell array. The cell array contains the indices for all elements
in A that are within tolerance of a value in C.
That is, each cell in IA corresponds to a value
in C, and the values in each cell correspond to
locations in A.
Example: [C,IA] = uniquetol(A,tol,'OutputAllIndices',true)
Row comparison toggle, specified as the comma-separated pair
consisting of 'ByRows' and either false (default), true, 0,
or 1. uniquetol interprets
numeric 0 as false and numeric 1 as true.
Use this option to find rows in A that are unique,
within tolerance.
When ByRows is true:
Amust be a 2-D array.uniquetolcompares the rows ofAby considering each column separately. For two rows to be within tolerance of one another, each column has to be in tolerance.Each row in
Ais within tolerance of a row inC. However, no two rows inCare within tolerance of each other.
Two rows, u and v, are
within tolerance if all(abs(u-v) <= tol*max(abs(A),[],1)).
Example: C = uniquetol(A,tol,'ByRows',true)
Scale of data, specified as the comma-separated pair consisting
of 'DataScale' and either a scalar or vector.
Specify DataScale as a numeric scalar, DS,
to change the tolerance test to be abs(u-v) <= tol*DS.
When used together with the ByRows option,
the DataScale value also can be a vector. In this
case, each element of the vector specifies DS for
a corresponding column in A. If a value in the DataScale vector
is Inf, then uniquetol ignores
the corresponding column in A.
Example: C = uniquetol(A,'DataScale',1)
Example: [C,IA,IC] = uniquetol(A,'ByRows',true,'DataScale',[eps(1)
eps(10) eps(100)])
Data Types: single | double
Range preservation toggle, specified as the comma-separated pair
consisting of 'PreserveRange' and either
false (default), true,
0, or 1.
uniquetol interprets numeric
0 as false and numeric
1 as true. Use this option to
specify that the minimum and maximum values in the output
C should be the same as those in
A.
If the minimum and maximum values in A are within
the tolerance tol of each other, then
uniquetol returns only one of the
values.
Example: C =
uniquetol(A,tol,'PreserveRange',true)
Output Arguments
Unique elements in A (within tolerance),
returned as a vector or matrix. If A is a row vector,
then C is also a row vector. Otherwise, C is
a column vector. The elements in C are sorted in
ascending order. Each element in A is within tolerance
of an element in C, but no two elements in C are
within tolerance of each other.
If the ByRows option is true,
then C is a matrix containing the unique rows in A.
In this case, the rows in C are sorted in ascending
order by the first column. Each row in A is within
tolerance of a row in C, but no two rows in C are
within tolerance of each other.
Index to A, returned as a column vector of
indices to the first occurrence of repeated elements, or as a cell
array. IA generally satisfies C = A(IA),
with the following exceptions:
If the
ByRowsoption istrue, thenC = A(IA,:).If the
OutputAllIndicesoption istrue, thenIAis a cell array andC(i)~A(IA{i})where~means the values are within tolerance of each other.
Index to C, returned as a column vector of
indices. IC satisfies the following properties,
where ~ means the values are within tolerance of
each other.
If
Ais a vector, thenA~C(IC).If
Ais a matrix, thenA(:)~C(IC).If the
ByRowsoption istrue, thenA~C(IC,:).
Algorithms
uniquetol sorts the input lexicographically, and then starts at
the lowest or highest value to find unique values within tolerance. As a result,
changing the sorting of the input could change the output. For example,
uniquetol(-A) might not give the same results as
-uniquetol(A).
There can be multiple valid C outputs that satisfy the condition,
no two elements in C are within tolerance of each
other. The uniquetol function can return several of
the valid outputs, depending on whether the value of occurrence is
'highest' or 'lowest' and whether the
PreserveRange option is specified.
Extended Capabilities
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The uniquetol function
supports GPU array input with these usage notes and limitations:
The
occurrenceargument for occurrence of unique values is not supported.The
'ByRows','OutputAllIndices', and'PreserveRange'options are not supported.64-bit integers are not supported.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2015aThe occurrence argument controls whether the algorithm begins
with the highest or lowest elements in the input data. The
'PreserveRange' name-value argument specifies whether the
range of the output data should be the same as the input data.
See Also
unique | isapprox | ismembertol | ismember | eps
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)