Average Similar Data Points Using a Tolerance
This example shows how to use uniquetol to find the average z-coordinate of 3-D points that have similar (within tolerance) x and y coordinates.
Use random points picked from the peaks function in the domain as the data set. Add a small amount of noise to the data.
xy = rand(10000,2)*6-3;
z = peaks(xy(:,1),xy(:,2)) + 0.5-rand(10000,1);
A = [xy z];
plot3(A(:,1), A(:,2), A(:,3), '.')
view(-28,32)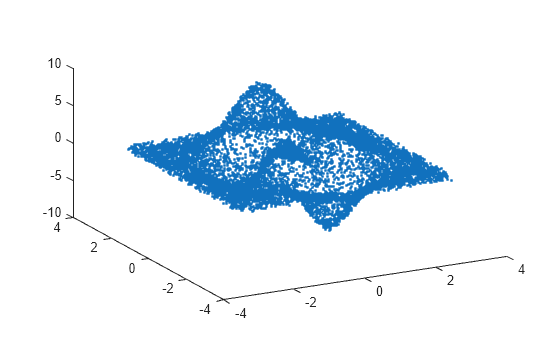
Find points that have similar x and y coordinates using uniquetol with these options:
Specify
ByRowsastrue, since the rows ofAcontain the point coordinates.Specify
OutputAllIndicesastrueto return the indices for all points that are within tolerance of each other.Specify
DataScaleas[1 1 Inf]to use an absolute tolerance for thexandycoordinates, while ignoring thez-coordinate.
DS = [1 1 Inf]; [C,ia] = uniquetol(A, 0.3, 'ByRows', true, ... 'OutputAllIndices', true, 'DataScale', DS);
Average each group of points that are within tolerance (including the z-coordinates), producing a reduced data set that still holds the general shape of the original data.
for k = 1:length(ia) aveA(k,:) = mean(A(ia{k},:),1); end
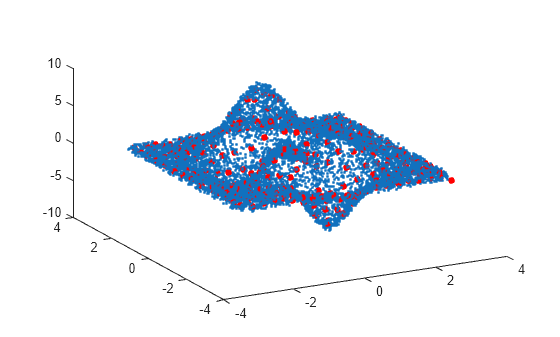
Plot the resulting averaged-out points on top of the original data.
hold on plot3(aveA(:,1), aveA(:,2), aveA(:,3), '.r', 'MarkerSize', 15)