Extract Linear Controller from MPC Controller
This example shows how to obtain an LTI representation of an unconstrained MPC controller using ss. You can use this to analyze the frequency response and performance of the controller.
Define a plant model. For this example, use the CSTR model described in Design Controller Using MPC Designer.
A = [-5 -0.3427; 47.68 2.785]; B = [0 1; 0.3 0]; C = [0 1; 1 0]; D = zeros(2,2); CSTR = ss(A,B,C,D);
Define inputs and outputs for MPC (see also setmpcsignals).
CSTR.InputGroup.MV = 1; % coolant temperature (K) CSTR.InputGroup.UD = 2; % inflow reagent concentration (kmol/m^3) CSTR.OutputGroup.MO = 1; % reactor temperature (K) CSTR.OutputGroup.UO = 2; % key reactant concentration (kmol/m^3)
Create an MPC controller for the defined plant using the same sample time, prediction horizon, and tuning weights described in Design MPC Controller at the Command Line.
mpcobj = mpc(CSTR,1,15);
-->"ControlHorizon" is empty. Assuming default 2. -->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000. for output(s) y1 and zero weight for output(s) y2
mpcobj.W.ManipulatedVariablesRate = 0.3; mpcobj.W.OutputVariables = [1 0];
Compute the steady-state output sensitivity (also known as complementary sensitivity) gain matrix for the closed loop system.
DCgain = cloffset(mpcobj)
-->Converting model to discrete time. -->The "Model.Disturbance" property is empty: Assuming unmeasured input disturbance #2 is integrated white noise. Assuming no disturbance added to measured output #1. -->"Model.Noise" is empty. Assuming white noise on each measured output.
DCgain = 1.3323e-15
Extract the LTI state-space representation of the controller.
MPCss = ss(mpcobj);
Convert the original CSTR model to discrete-time using the same sample time of the MPC controller.
CSTRd = c2d(CSTR,MPCss.Ts);
Create an LTI model of the closed-loop system using feedback. Use the manipulated variable and measured output for feedback, indicating that the feedback signal is added to the input (not subtracted). Subtracting the feedback signal from the input would lead to an unstable closed-loop system, because the MPC controller is designed using an additive feedback signal convention.
clsys = feedback(CSTRd,MPCss,1,1,1);
You can then analyze the resulting feedback system. For example, verify that all closed-loop poles are within the unit circle.
poles = eig(clsys)
poles = 6×1 complex
-0.4033 + 0.0000i
0.0323 + 0.3177i
0.0323 - 0.3177i
0.2402 + 0.0000i
-0.0558 + 0.0000i
0.0390 + 0.0000i
Display the magnitude and damping of all the poles.
damp(clsys)
Pole Magnitude Damping Frequency Time Constant
(rad/seconds) (seconds)
2.40e-01 2.40e-01 1.00e+00 1.43e+00 7.01e-01
3.23e-02 + 3.18e-01i 3.19e-01 6.14e-01 1.86e+00 8.76e-01
3.23e-02 - 3.18e-01i 3.19e-01 6.14e-01 1.86e+00 8.76e-01
3.90e-02 3.90e-02 1.00e+00 3.24e+00 3.08e-01
-4.03e-01 4.03e-01 2.78e-01 3.27e+00 1.10e+00
-5.58e-02 5.58e-02 6.76e-01 4.27e+00 3.47e-01
Display the transmission zeros.
tzero(clsys)
ans = 4×1
-0.2360
-0.0336
0.0249
1.0000
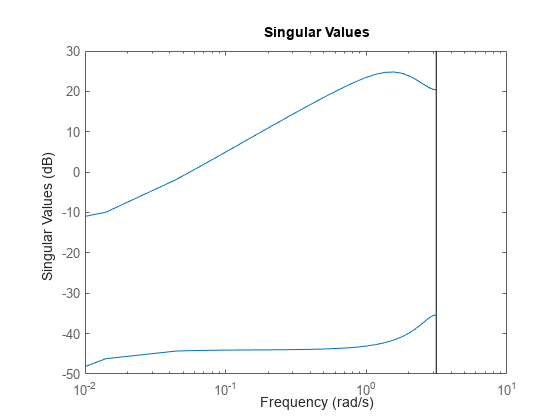
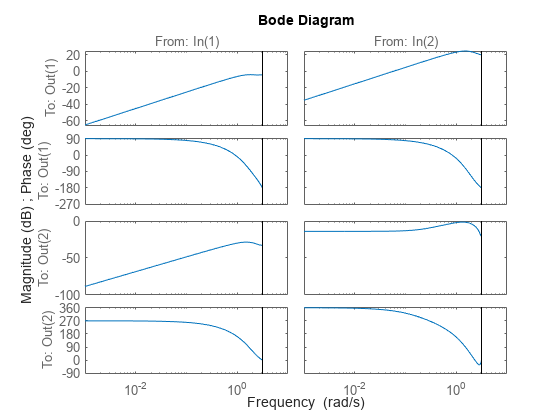
You can also plot its singular values, or view the frequency responses of each channel.
sigma(clsys)
bode(clsys)
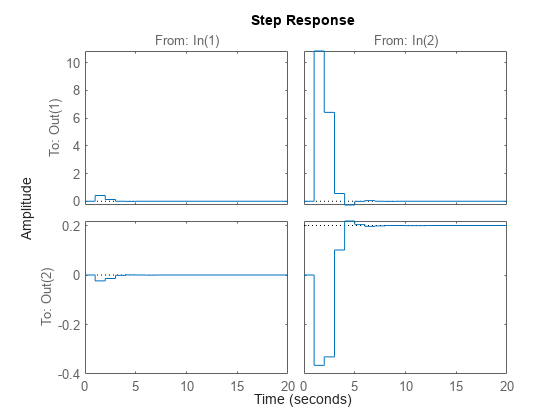
Display the step responses of each channel.
step(clsys)
Display the DC gain matrix (from the system input to the system output) of the closed loop system. This matrix is related to the steady state complementary sensitivity previously calculated with cloffset.
dcgain(clsys)
ans = 2×2
0.0000 0.0000
-0.0000 0.2000
See Also
Functions
ss|feedback|getindist|getoutdist|setindist|setoutdist|getEstimator|setEstimator