fsolve
Solve system of nonlinear equations
Syntax
Description
Nonlinear system solver
Solves a problem specified by
F(x) = 0
for x, where F(x) is a function that returns a vector value.
x is a vector or a matrix; see Matrix Arguments.
x = fsolve(fun,x0)x0 and tries to solve the equations fun(x) = 0,
an array of zeros.
Note
Passing Extra Parameters explains how
to pass extra parameters to the vector function fun(x),
if necessary. See Solve Parameterized Equation.
x = fsolve(fun,x0,options)options.
Use optimoptions to set these
options.
Examples
This example shows how to solve two nonlinear equations in two variables. The equations are
Convert the equations to the form .
The root2d.m function, which is available when you run this example, computes the values.
type root2d.mfunction F = root2d(x) F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2); F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
Solve the system of equations starting at the point [0,0].
fun = @root2d; x0 = [0,0]; x = fsolve(fun,x0)
Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
x = 1×2
0.3532 0.6061
Examine the solution process for a nonlinear system.
Set options to have no display and a plot function that displays the first-order optimality, which should converge to 0 as the algorithm iterates.
options = optimoptions('fsolve','Display','none','PlotFcn',@optimplotfirstorderopt);
The equations in the nonlinear system are
Convert the equations to the form .
The root2d function computes the left-hand side of these two equations.
type root2d.mfunction F = root2d(x) F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2); F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
Solve the nonlinear system starting from the point [0,0] and observe the solution process.
fun = @root2d; x0 = [0,0]; x = fsolve(fun,x0,options)
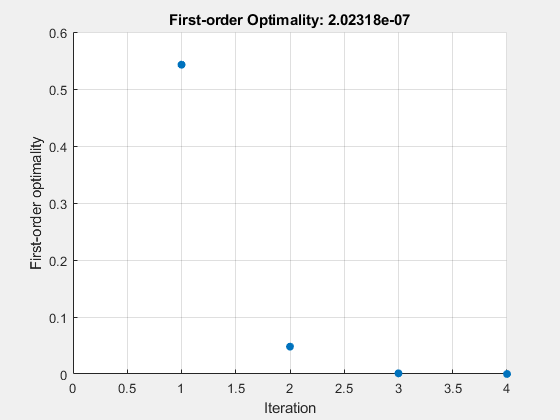
x = 1×2
0.3532 0.6061
You can parameterize equations as described in the topic Passing Extra Parameters. For example, the paramfun helper function at the end of this example creates the following equation system parameterized by :
To solve the system for a particular value, in this case , set in the workspace and create an anonymous function in x from paramfun.
c = -1; fun = @(x)paramfun(x,c);
Solve the system starting from the point x0 = [0 1].
x0 = [0 1]; x = fsolve(fun,x0)
Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
x = 1×2
0.1976 0.4255
To solve for a different value of , enter in the workspace and create the fun function again, so it has the new value.
c = -2;
fun = @(x)paramfun(x,c); % fun now has the new c value
x = fsolve(fun,x0)Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
x = 1×2
0.1788 0.3418
Helper Function
This code creates the paramfun helper function.
function F = paramfun(x,c) F = [ 2*x(1) + x(2) - exp(c*x(1)) -x(1) + 2*x(2) - exp(c*x(2))]; end
Create a problem structure for fsolve and solve the problem.
Solve the same problem as in Solution with Nondefault Options, but formulate the problem using a problem structure.
Set options for the problem to have no display and a plot function that displays the first-order optimality, which should converge to 0 as the algorithm iterates.
problem.options = optimoptions('fsolve','Display','none','PlotFcn',@optimplotfirstorderopt);
The equations in the nonlinear system are
Convert the equations to the form .
The root2d function computes the left-hand side of these two equations.
type root2dfunction F = root2d(x) F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2); F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
Create the remaining fields in the problem structure.
problem.objective = @root2d;
problem.x0 = [0,0];
problem.solver = 'fsolve';Solve the problem.
x = fsolve(problem)
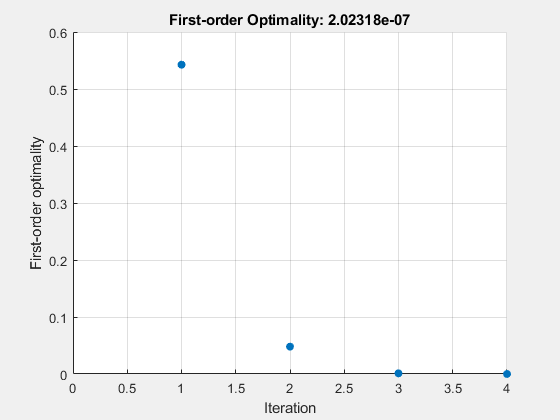
x = 1×2
0.3532 0.6061
This example returns the iterative display showing the solution process for the system of two equations and two unknowns
Rewrite the equations in the form :
Start your search for a solution at x0 = [-5 -5].
First, write a function that computes F, the values of the equations at x.
F = @(x) [2*x(1) - x(2) - exp(-x(1));
-x(1) + 2*x(2) - exp(-x(2))];Create the initial point x0.
x0 = [-5;-5];
Set options to return iterative display.
options = optimoptions('fsolve','Display','iter');
Solve the equations.
[x,fval] = fsolve(F,x0,options)
Norm of First-order Trust-region
Iteration Func-count ||f(x)||^2 step optimality radius
0 3 47071.2 2.29e+04 1
1 6 12003.4 1 5.75e+03 1
2 9 3147.02 1 1.47e+03 1
3 12 854.452 1 388 1
4 15 239.527 1 107 1
5 18 67.0412 1 30.8 1
6 21 16.7042 1 9.05 1
7 24 2.42788 1 2.26 1
8 27 0.032658 0.759511 0.206 2.5
9 30 7.03149e-06 0.111927 0.00294 2.5
10 33 3.29525e-13 0.00169132 6.36e-07 2.5
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.
<stopping criteria details>
x = 2×1
0.5671
0.5671
fval = 2×1
10-6 ×
-0.4059
-0.4059
The iterative display shows f(x), which is the square of the norm of the function F(x). This value decreases to near zero as the iterations proceed. The first-order optimality measure likewise decreases to near zero as the iterations proceed. These entries show the convergence of the iterations to a solution. For the meanings of the other entries, see Iterative Display.
The fval output gives the function value F(x), which should be zero at a solution (to within the FunctionTolerance tolerance).
Find a matrix that satisfies
,
starting at the point x0 = [1,1;1,1]. Create an anonymous function that calculates the matrix equation and create the point x0.
fun = @(x)x*x*x - [1,2;3,4]; x0 = ones(2);
Set options to have no display.
options = optimoptions('fsolve','Display','off');
Examine the fsolve outputs to see the solution quality and process.
[x,fval,exitflag,output] = fsolve(fun,x0,options)
x = 2×2
-0.1291 0.8602
1.2903 1.1612
fval = 2×2
10-9 ×
-0.2742 0.1258
0.1876 -0.0864
exitflag = 1
output = struct with fields:
iterations: 11
funcCount: 52
algorithm: 'trust-region-dogleg'
firstorderopt: 4.0197e-10
message: 'Equation solved.↵↵fsolve completed because the vector of function values is near zero↵as measured by the value of the function tolerance, and↵the problem appears regular as measured by the gradient.↵↵<stopping criteria details>↵↵Equation solved. The sum of squared function values, r = 1.336702e-19, is less than↵sqrt(options.FunctionTolerance) = 1.000000e-03. The relative norm of the gradient of r,↵4.019681e-10, is less than options.OptimalityTolerance = 1.000000e-06.'
The exit flag value 1 indicates that the solution is reliable. To verify this manually, calculate the residual (sum of squares of fval) to see how close it is to zero.
sum(sum(fval.*fval))
ans = 1.3367e-19
This small residual confirms that x is a solution.
You can see in the output structure how many iterations and function evaluations fsolve performed to find the solution.
Input Arguments
Nonlinear equations to solve, specified as a function handle
or function name. fun is a function that accepts
a vector x and returns a vector F,
the nonlinear equations evaluated at x. The equations
to solve are F = 0
for all components of F. The function fun can
be specified as a function handle for a file
x = fsolve(@myfun,x0)
where myfun is a MATLAB® function such
as
function F = myfun(x) F = ... % Compute function values at x
fun can also be a function handle for an
anonymous function.
x = fsolve(@(x)sin(x.*x),x0);
fsolve passes x to your objective function in the shape of the x0 argument. For example, if x0 is a 5-by-3 array, then fsolve passes x to fun as a 5-by-3 array.
If the Jacobian can also be computed and the
'SpecifyObjectiveGradient' option is
true, set by
options = optimoptions('fsolve','SpecifyObjectiveGradient',true)
the function fun must return, in a second
output argument, the Jacobian value J, a matrix,
at x.
If fun returns a vector (matrix) of m components
and x has length n, where n is
the length of x0, the Jacobian J is
an m-by-n matrix where J(i,j) is
the partial derivative of F(i) with respect to x(j).
(The Jacobian J is the transpose of the gradient
of F.)
Example: fun = @(x)x*x*x-[1,2;3,4]
Data Types: char | function_handle | string
Initial point, specified as a real vector or real array. fsolve uses
the number of elements in and size of x0 to determine
the number and size of variables that fun accepts.
Example: x0 = [1,2,3,4]
Data Types: double
Optimization options, specified as the output of optimoptions or
a structure such as optimset returns.
Some options apply to all algorithms, and others are relevant for particular algorithms. See Optimization Options Reference for detailed information.
Some options are absent from the
optimoptions display. These options appear in italics in the following
table. For details, see View Optimization Options.
| All Algorithms | |
Algorithm | Choose between The To
set some algorithm options using
|
| CheckGradients | Compare user-supplied derivatives (gradients of objective or
constraints) to finite-differencing derivatives. The
choices are For
The |
| Diagnostics | Display diagnostic information
about the function to be minimized or solved. The choices are |
| DiffMaxChange | Maximum change in variables for
finite-difference gradients (a positive scalar). The default is |
| DiffMinChange | Minimum change in variables for
finite-difference gradients (a positive scalar). The default is |
Display | Level of display (see Iterative Display):
|
FiniteDifferenceStepSize | Scalar or vector step size factor for finite differences. When
you set
sign′(x) = sign(x) except sign′(0) = 1.
Central finite differences are
FiniteDifferenceStepSize expands to a vector. The default
is sqrt(eps) for forward finite differences, and eps^(1/3)
for central finite differences.
For |
FiniteDifferenceType | Finite differences, used to estimate gradients,
are either The algorithm is careful to obey bounds when estimating both types of finite differences. So, for example, it could take a backward, rather than a forward, difference to avoid evaluating at a point outside bounds. For |
FunctionTolerance | Termination tolerance on the function value, a nonnegative
scalar. The default is For |
| FunValCheck | Check whether objective function
values are valid. |
MaxFunctionEvaluations | Maximum number of function evaluations allowed, a nonnegative
integer. The default is
For |
MaxIterations | Maximum number of iterations allowed, a nonnegative integer. The
default is For |
OptimalityTolerance | Termination tolerance on the first-order optimality (a
nonnegative scalar). The default is Internally,
the |
OutputFcn | Specify one or more user-defined functions that an optimization
function calls at each iteration. Pass a function handle
or a cell array of function handles. The default is none
( |
PlotFcn | Plots various measures of progress while the algorithm executes;
select from predefined plots or write your own. Pass a
built-in plot function name, a function handle, or a
cell array of built-in plot function names or function
handles. For custom plot functions, pass function
handles. The default is none
(
Custom plot functions use the same syntax as output functions. See Output Functions for Optimization Toolbox and Output Function and Plot Function Syntax. For
|
SpecifyObjectiveGradient | If For |
StepTolerance | Termination tolerance on For |
TypicalX | Typical The |
UseParallel | When |
| trust-region Algorithm | |
JacobianMultiplyFcn | Jacobian multiply function, specified as a function handle. For
large-scale structured problems, this function computes
the Jacobian matrix product W = jmfun(Jinfo,Y,flag) where
[F,Jinfo] = fun(x)
In each case, Note
See Minimization with Dense Structured Hessian, Linear Equalities for a similar example. For
|
| JacobPattern | Sparsity pattern of the Jacobian
for finite differencing. Set Use In
the worst case, if the structure is unknown, do not set |
| MaxPCGIter | Maximum number of PCG (preconditioned
conjugate gradient) iterations, a positive scalar. The default is |
| PrecondBandWidth | Upper bandwidth of preconditioner
for PCG, a nonnegative integer. The default |
SubproblemAlgorithm | Determines how the iteration step
is calculated. The default, |
| TolPCG | Termination tolerance on the PCG
iteration, a positive scalar. The default is |
| Levenberg-Marquardt Algorithm | |
| InitDamping | Initial value of the Levenberg-Marquardt parameter,
a positive scalar. Default is |
| ScaleProblem |
|
Example: options = optimoptions('fsolve','FiniteDifferenceType','central')
Problem structure, specified as a structure with the following fields:
| Field Name | Entry |
|---|---|
| Objective function |
| Initial point for x |
| 'fsolve' |
| Options created with optimoptions |
Data Types: struct
Output Arguments
Solution, returned as a real vector or real array. The size
of x is the same as the size of x0.
Typically, x is a local solution to the problem
when exitflag is positive. For information on
the quality of the solution, see When the Solver Succeeds.
Objective function value at the solution, returned as a real vector. Generally,
fval = fun(x).
Reason fsolve stopped, returned as an integer.
| Equation solved. First-order optimality is small. |
| Equation solved. Change in |
| Equation solved. Change in residual smaller than the specified tolerance. |
| Equation solved. Magnitude of search direction smaller than specified tolerance. |
| Number of iterations exceeded |
| Output function or plot function stopped the algorithm. |
| Equation not solved. The exit message can have more information. |
| Equation not solved. Trust region radius became too small
( |
Information about the optimization process, returned as a structure with fields:
iterations | Number of iterations taken |
funcCount | Number of function evaluations |
algorithm | Optimization algorithm used |
cgiterations | Total number of PCG iterations ( |
stepsize | Final displacement in |
firstorderopt | Measure of first-order optimality |
message | Exit message |
Jacobian at the solution, returned as a real matrix. jacobian(i,j) is
the partial derivative of fun(i) with respect to x(j) at
the solution x.
For problems with active constraints at the solution, jacobian is
not useful for estimating confidence intervals.
Limitations
The function to be solved must be continuous.
When successful,
fsolveonly gives one root.The default trust-region dogleg method can only be used when the system of equations is square, i.e., the number of equations equals the number of unknowns. For the Levenberg-Marquardt method, the system of equations need not be square.
More About
The next few items list the possible enhanced exit messages from
fsolve. Enhanced exit messages give a link for more
information as the first sentence of the message.
The solver found a point where the sum of squares of function values is less than
the square root of the FunctionTolerance
tolerance. The gradient of
the sum of squares is also less than OptimalityTolerance
(1e-4*OptimalityTolerance for the Levenberg-Marquardt
algorithm).
For suggestions on how to proceed, see When the Solver Succeeds.
The initial point seems to be a solution of the equation, because the sum of
squares of function values is less than the square root of the FunctionTolerance
tolerance. The size of the
gradient of the sum of squares is also less than OptimalityTolerance
(1e-4*OptimalityTolerance for the Levenberg-Marquardt
algorithm).
For suggestions on how to proceed, see Final Point Equals Initial Point.
The solver found a point where the sum of squares of function values is less than the square root of the FunctionTolerance tolerance. However, the last step was less than the StepTolerance tolerance, indicating the function may be changing rapidly, or that the function is not smooth near the final point. This is the meaning of stalled.
For suggestions on how to proceed, see Local Minimum Possible.
The solver found a point where the sum of squares of function values is less than
the square root of the FunctionTolerance
tolerance. However, the
sum of squares changed very little in the last step, even though the gradient of the
sum was larger than OptimalityTolerance
(1e-4*OptimalityTolerance for the Levenberg-Marquardt
algorithm). This can indicate that the reported point is not near a solution.
For suggestions on how to proceed, see Local Minimum Possible.
The solver is unable to further reduce the sum of squares of function values, but this sum exceeds the square root of the FunctionTolerance tolerance.
For suggestions on how to proceed, see fsolve Could Not Solve Equation.
The next few items contain definitions for terms in the fsolve exit messages.
To solve a system of equations F(x) = 0, the solver generally attempts to minimize the sum of squared function values r = Σ(Fi(x))2. Both r and ∇r should be zero at a solution.
Generally, a tolerance is a threshold which, if crossed, stops the iterations of a solver. For more information on tolerances, see Tolerances and Stopping Criteria.
The tolerance called OptimalityTolerance relates to the
first-order optimality measure. Iterations end when the first-order optimality
measure is less than OptimalityTolerance.
The first-order optimality measure is the size of the gradient of the sum of squares of function values. This should be zero at the root of a smooth function.
The function tolerance called
FunctionTolerance relates to the size of the latest change in
sum of squares of function values.

StepTolerance is a tolerance for the size of
the last step, meaning the size of the change in location where
fsolve was evaluated.

The problem appears to be regular means the size of the gradient of the sum of
squares of function values is less than the OptimalityTolerance
tolerance
(1e-4*OptimalityTolerance for the Levenberg-Marquardt
algorithm).
The solver was unable to reduce the sum of squares of function values to below the square root of the FunctionTolerance tolerance. Its last iteration did not reduce the sum of squares enough to warrant further attempts.
For suggestions on how to proceed, see fsolve Could Not Solve Equation.
The trust region is too small to continue. This could be because the sum of squares of function values is not close to a quadratic model. For more information, see Trust-Region-Dogleg Algorithm.
The trust region is too small to continue. This could be because the sum of squares of function values is not close to a quadratic model. For more information, see Trust-Region-Dogleg Algorithm.
The Levenberg-Marquardt regularization parameter is related to the inverse of a trust-region radius. It becomes large when the sum of squares of function values is not close to a quadratic model. For more information, see Levenberg-Marquardt Method.
Tips
For large problems, meaning those with thousands of variables or more, save memory (and possibly save time) by setting the
Algorithmoption to'trust-region'and theSubproblemAlgorithmoption to'cg'.
Algorithms
The Levenberg-Marquardt and trust-region methods are based on
the nonlinear least-squares algorithms also used in lsqnonlin. Use one of these methods if
the system may not have a zero. The algorithm still returns a point
where the residual is small. However, if the Jacobian of the system
is singular, the algorithm might converge to a point that is not a
solution of the system of equations (see Limitations).
By default
fsolvechooses the trust-region dogleg algorithm. The algorithm is a variant of the Powell dogleg method described in [8]. It is similar in nature to the algorithm implemented in [7]. See Trust-Region-Dogleg Algorithm.The trust-region algorithm is a subspace trust-region method and is based on the interior-reflective Newton method described in [1] and [2]. Each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradients (PCG). See Trust-Region Algorithm.
The Levenberg-Marquardt method is described in references [4], [5], and [6]. See Levenberg-Marquardt Method.
Alternative Functionality
App
The Optimize Live Editor task provides a visual interface for fsolve.
References
[1] Coleman, T.F. and Y. Li, “An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds,” SIAM Journal on Optimization, Vol. 6, pp. 418-445, 1996.
[2] Coleman, T.F. and Y. Li, “On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds,” Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.
[3] Dennis, J. E. Jr., “Nonlinear Least-Squares,” State of the Art in Numerical Analysis, ed. D. Jacobs, Academic Press, pp. 269-312.
[4] Levenberg, K., “A Method for the Solution of Certain Problems in Least-Squares,” Quarterly Applied Mathematics 2, pp. 164-168, 1944.
[5] Marquardt, D., “An Algorithm for Least-squares Estimation of Nonlinear Parameters,” SIAM Journal Applied Mathematics, Vol. 11, pp. 431-441, 1963.
[6] Moré, J. J., “The Levenberg-Marquardt Algorithm: Implementation and Theory,” Numerical Analysis, ed. G. A. Watson, Lecture Notes in Mathematics 630, Springer Verlag, pp. 105-116, 1977.
[7] Moré, J. J., B. S. Garbow, and K. E. Hillstrom, User Guide for MINPACK 1, Argonne National Laboratory, Rept. ANL-80-74, 1980.
[8] Powell, M. J. D., “A Fortran Subroutine for Solving Systems of Nonlinear Algebraic Equations,” Numerical Methods for Nonlinear Algebraic Equations, P. Rabinowitz, ed., Ch.7, 1970.
Extended Capabilities
fsolvesupports code generation using either thecodegen(MATLAB Coder) function or the MATLAB Coder™ app. You must have a MATLAB Coder license to generate code.The target hardware must support standard double-precision floating-point computations. You cannot generate code for single-precision or fixed-point computations.
Code generation targets do not use the same math kernel libraries as MATLAB solvers. Therefore, code generation solutions can vary from solver solutions, especially for poorly conditioned problems.
All code for generation must be MATLAB code. In particular, you cannot use a custom black-box function as an objective function for
fsolve. You can usecoder.cevalto evaluate a custom function coded in C or C++. However, the custom function must be called in a MATLAB function.Code generation does not support complex-valued data.
fsolvedoes not support theproblemargument for code generation.[x,fval] = fsolve(problem) % Not supportedYou must specify the objective function by using function handles, not strings or character names.
x = fsolve(@fun,x0,options) % Supported % Not supported: fsolve('fun',...) or fsolve("fun",...)
For advanced code optimization involving embedded processors, you also need an Embedded Coder® license.
You must include options for
fsolveand specify them usingoptimoptions. The options must include theAlgorithmoption, set to'levenberg-marquardt'.options = optimoptions('fsolve','Algorithm','levenberg-marquardt'); [x,fval,exitflag] = fsolve(fun,x0,options);
Code generation supports these options:
Algorithm— Must be'levenberg-marquardt'FiniteDifferenceStepSizeFiniteDifferenceTypeFunctionToleranceMaxFunctionEvaluationsMaxIterationsSpecifyObjectiveGradientStepToleranceTypicalX
Generated code has limited error checking for options. The recommended way to update an option is to use
optimoptions, not dot notation.opts = optimoptions('fsolve','Algorithm','levenberg-marquardt'); opts = optimoptions(opts,'MaxIterations',1e4); % Recommended opts.MaxIterations = 1e4; % Not recommended
Do not load options from a file. Doing so can cause code generation to fail. Instead, create options in your code.
Usually, if you specify an option that is not supported, the option is silently ignored during code generation. However, if you specify a plot function or output function by using dot notation, code generation can issue an error. For reliability, specify only supported options.
Because output functions and plot functions are not supported, solvers do not return the exit flag –1.
For an example, see Generate Code for fsolve.
To run in parallel, set the 'UseParallel' option to true.
options = optimoptions('solvername','UseParallel',true)
For more information, see Using Parallel Computing in Optimization Toolbox.
Version History
Introduced before R2006aThe syntax for the JacobianMultiplyFcn option is
W = jmfun(Jinfo, Y, flag)
The Jinfo data, which MATLAB passes to your function jmfun, can now be of any
data type. For example, you can now have Jinfo be a structure. In
previous releases, Jinfo had to be a standard double
array.
The Jinfo data is the second output of your objective
function:
[F,Jinfo] = myfun(x)
The CheckGradients option will be removed in a future release. To check the first derivatives of objective functions or nonlinear constraint functions, use the checkGradients function.
See Also
fzero | lsqcurvefit | lsqnonlin | optimoptions | Optimize
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)