evaluateHeatFlux
Evaluate heat flux of thermal solution at nodal or arbitrary spatial locations
Syntax
Description
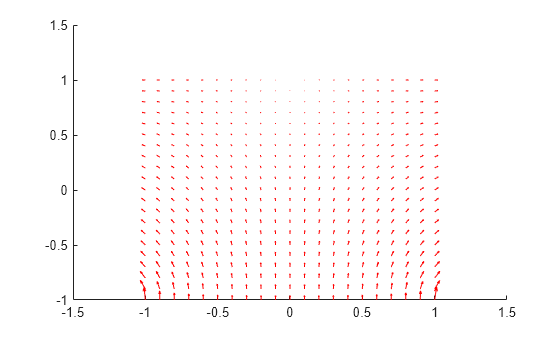
[ returns the heat
flux for a 2-D problem at the nodal points of the triangular mesh.qx,qy]
= evaluateHeatFlux(thermalresults)
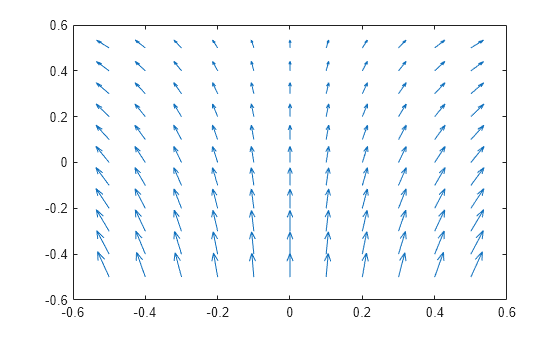
[ returns the heat
flux for a 3-D thermal problem at the nodal points of the tetrahedral
mesh.qx,qy,qz]
= evaluateHeatFlux(thermalresults)
[
returns the heat flux for a thermal problem at the 2-D points specified in
qx,qy]
= evaluateHeatFlux(thermalresults,xq,yq)xq and yq. This syntax is valid for
both the steady-state and transient thermal models.
[___] = evaluateHeatFlux(
returns the heat flux for a thermal problem at the 2-D or 3-D points specified
in thermalresults,querypoints)querypoints. This syntax is valid for both the
steady-state and transient thermal models.
[___] = evaluateHeatFlux(___,
returns the heat flux for a thermal problem at the times specified in
iT)iT. You can specify iT after the
input arguments in any of the previous syntaxes.
The first dimension of qx, qy, and,
in the 3-D case, qz represents the node indices or
corresponds to query points. The second dimension corresponds to time steps
iT.
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2017a