npwgnthresh
Detection SNR threshold for signal in white Gaussian noise
Syntax
Description
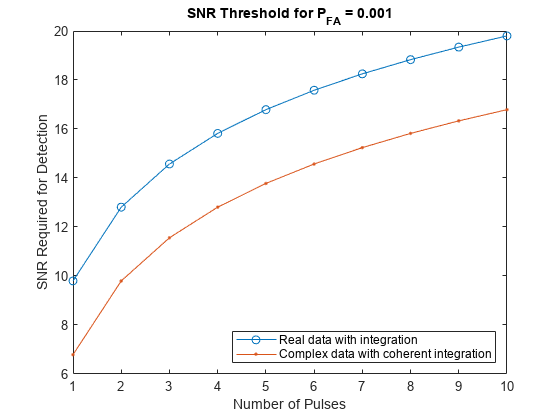
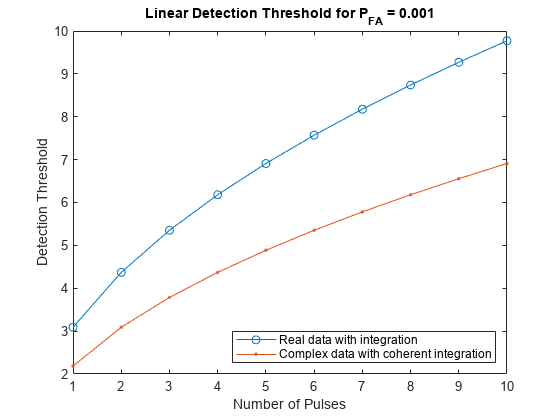
snrthresh = npwgnthresh(pfa)pfa. This function uses a square-law detector.
Examples
Input Arguments
Output Arguments
More About
References
[1] Kay, S. M. Fundamentals of Statistical Signal Processing: Detection Theory. Upper Saddle River, NJ: Prentice Hall, 1998.
[2] Richards, M. A. Fundamentals of Radar Signal Processing. New York: McGraw-Hill, 2005.
Extended Capabilities
Version History
Introduced in R2011a