phased.URA
Uniform rectangular array
Description
To create a Uniform Rectangular Array (URA) System object™:
Create the
phased.URAobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
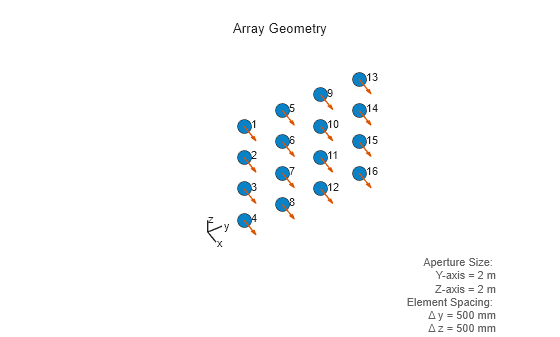
array = phased.URAarray (URA) System object that models a URA formed from identical isotropic phased array elements.
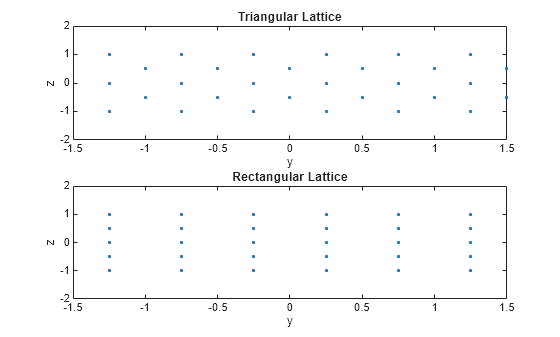
Array elements are contained in the yz-plane in a
rectangular lattice. The array look direction (boresight) points along the positive
x-axis.
array = phased.URA(Name,Value)array object with each specified property Name set to the
specified Value. You can specify additional name-value pair arguments in any order as
(Name1,Value1, ...,
NameN,ValueN). All properties needed to fully
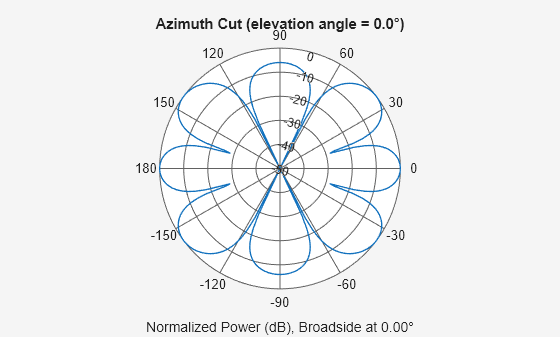
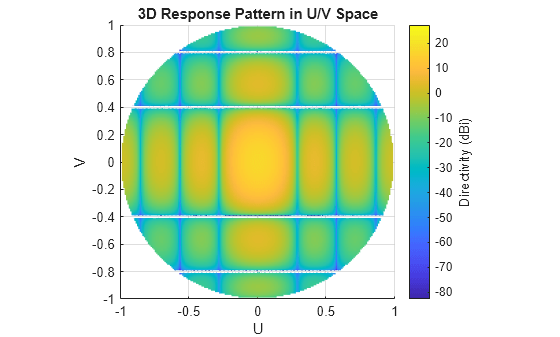
specify this object can be found in Properties.Response of 2-by-2 URA of Short-Dipole Antennas
array = phased.URA(SZ,D,Name,Value)phased.URA
array
System object with its Size property set to SZ
and its ElementSpacing property set to D. Other
specified property Names are set to the specified Values. SZ and
D are value-only arguments. When specifying a value-only argument,
specify all preceding value-only arguments. You can specify name-value pair arguments in
any order.
Properties
Usage
Syntax
Description
RESP = array(FREQ,ANG)RESP, at the operating
frequencies specified in FREQ and directions specified in
ANG.
Note
The object performs an initialization the first time the object is executed. This
initialization locks nontunable properties
and input specifications, such as dimensions, complexity, and data type of the input data.
If you change a nontunable property or an input specification, the System object issues an error. To change nontunable properties or inputs, you must first
call the release method to unlock the object.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
References
[1] Brookner, E., ed. Radar Technology. Lexington, MA: LexBook, 1996.
[2] Brookner, E., ed. Practical Phased Array Antenna Systems. Boston: Artech House, 1991.
[3] Mailloux, R. J. “Phased Array Theory and Technology,” Proceedings of the IEEE, Vol., 70, Number 3s, pp. 246–291.
[4] Mott, H. Antennas for Radar and Communications, A Polarimetric Approach. New York: John Wiley & Sons, 1992.
[5] Van Trees, H. Optimum Array Processing. New York: Wiley-Interscience, 2002.
Extended Capabilities
Version History
Introduced in R2011a